Cho f(1)=1, f(m+n)=f(m)+f(n)+mn với mọi mnÎN*. Tính giá trị của biểu thức T = log f 96 - f 69 - 241 2
A. 9
B. 3
C. 10
D. 4
Cho hàm số f(x) có f ( 1 ) = 1, f ( m + n ) = f ( m ) + f ( n ) + m n , ∀ m , n ∈ ℕ * . Giá trị của biểu thức T = log f ( 96 ) − f ( 69 ) − 241 2 là
A.4
B.3
C.6
D.9
Đáp án B.
Cho m=1 ta có
f ( n + 1 ) = f ( n ) + f ( 1 ) + n ⇔ f ( n + 1 ) = f ( n ) + n + 1.
Khi đó
f ( 2 ) + f ( 3 ) + ... + f ( k ) = f ( 1 ) + 2 + f ( 2 ) + 3 + ... + f ( k − 1 ) + k + 1
⇔ f ( 2 ) + f ( 3 ) + ... + f ( k − 1 ) + f ( k ) = f ( 1 ) + f ( 2 ) + ... + f ( k − 1 ) + ( 1 + 2 + ... + k )
⇔ f ( k ) = f ( 1 ) + ( 1 + 2 + ... + k ) = 1 + k ( k + 1 ) 2 .
Vậy hàm cần tìm là
f ( x ) = 1 + x ( x + 1 ) 2 ⇒ f ( 96 ) = 1 + 96.97 2 = 4657 f ( 69 ) = 1 + 69.70 2 = 2416
Vậy
T = log 4657 − 2416 − 241 2 = log 1000 = 3.
Cho hàm số f(x) có f ( 1 ) = 1 , f ( m + n ) = f ( m ) + f ( n ) + m n , ∀ m , n ∈ ℕ * . Giá trị của biểu thức T = log f ( 96 ) − f ( 69 ) − 241 2 là
A. 4
B. 3
C. 6
D. 9
Cho f(1) = 1; f(m + n) = f(m) + f( n) + m.n với các số nguyên dương m; n .Khi đó giá trị của biểu thức T = log f 2017 - f 2016 - 17 2 là
A. 3
B. 4
C. 6
D. 9
Chọn A.
Áp dụng hệ thức f(m + n) = f( m) + f( n) + mn
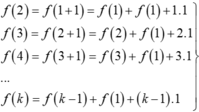
![]()
![]()
Vậy f( 2017) = 2017 + 2016.2017/2 = 20352153
f( 2016) = 2016 + 2015 + 2016/2 = 2033136

Cho đa thức f (x) thỏa mãn f(x) + x.f(-x) = x+1 với mọi giá trị của x . Tính f(-1)
Cho đa thức f (x)= a\(x^2\) + bx + c thỏa mãn f(1)= f(-1).
Chứng minh rằng f(x)= f(-x)
Ta có :f(x) =0<=>a.0^2+b.0+c=0
<=>c=0
f(1)=a.1^2+b.1+c=a+b+c
f(-1)=a.(-1)^2 +b. (-1) =a-b+c
=>b=-b
=>b+b=0
=>2b=0
=>b=0
=>f(x)=ax^2
Vì x^2=(-x)^2 với mọi x
=>ax^2=a(-x)^2
=>f(x) =f(-x)
cho đa thức f(x) thỏa mãn f(x) + x. f(-x) = x + 1 với mọi giá trị của x. Tính f(1)
Giải:
\(*)\) Thay \(x=1\) vào đa thức ta có:
\(f\left(1\right)+1.f\left(-1\right)=1+1=2\)
\(\Rightarrow f\left(1\right)+f\left(-1\right)=2\) \((*)\)
\(*)\) Thay \(x=-1\) vào đa thức ta có:
\(f\left(-1\right)+\left(-1\right).f\left(1\right)=-1+1=0\)
\(\Rightarrow f\left(-1\right)=f\left(1\right).\) Thay vào \((*)\) ta được:
\(2.f\left(1\right)=2\Rightarrow f\left(1\right)=\dfrac{2}{2}=1\)
Vậy \(f\left(1\right)=1\)
Cho đa thức f(x) thỏa mãn: f(x) + x×f(x) = x+1 với mọi giá trị của x. Tính f(x)
Lời giải:
$f(x)+xf(x)=x+1, \forall x$
$\Leftrightarrow f(x)(1+x)=x+1, \forall x$
$\Leftrightarrow (x+1)[f(x)-1]=0, \forall x$
$\Rightarrow f(x)-1=0\Rightarrow f(x)=1$
Cho đa thức f(x) thỏa mãn f(x)+x.f(-x)=x+1 với mọi giá trị của x. Tính f(-1)
Ta có:f(x)=x+1-x.f(-x)
=>f(1)=2-f(-1)=>f(-1)=2-f(1)
f(-1)=-1+1+f(1)=f(1)
=>2f(-1)=2
=>f(-1)=1
Cho f(x) là 1 đa thức thỏa mãn 3f (x) + 2 f(1-x) = 2x + 9 với mọi x. Tìm giá trị của f(2).
Thay lần lượt \(x=2\) và \(x=-1\) vào biểu thức trên ta được hệ pt:
\(\left\{{}\begin{matrix}3f\left(2\right)+2f\left(-1\right)=13\\3f\left(-1\right)+2f\left(2\right)=7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}6f\left(-1\right)+9f\left(2\right)=39\\6f\left(-1\right)+4f\left(2\right)=14\end{matrix}\right.\)
\(\Leftrightarrow5f\left(2\right)=25\Rightarrow f\left(2\right)=5\)
Cho biểu thức f(x)= x+2/ x-1
Tìm giá trị của biến để cho vế phải có nghĩa
Tính f(7); f(1)
Tìm x để f(x)=1/4
Tìm x thuộc Z để f(x) có giá trị nguyên
Tìm x để f(x)> 0
Mn giúp mk vs ak
f(x) = \(\frac{x+2}{x-1}\)
b) Thay \(x=7\) vào biểu thức f(x), ta được:
f(x) = \(\frac{7+2}{7-1}\)
f(x) = \(\frac{9}{6}\)
f(x) = \(\frac{3}{2}.\)
+ Thay \(x=1\) vào biểu thức f(x), ta được:
f(x) = \(\frac{1+2}{1-1}\)
f(x) = \(\frac{3}{0}\)
Ta có tất cả mọi số đều không chia được cho 0.
=> f(x) không có giá trị nào.
Mình chỉ làm được câu này thôi nhé.
Chúc bạn học tốt!