Trong không gian Oxyz. Cho tứ diện đều ABCD có A(0;1;2) và hình chiếu vuông góc của A trên mặt phẳng (BCD) là H (4; -3;-2). Tọa độ tâm I của mặt cầu ngoại tiếp tứ diện ABCD.
A. I(3; -2;-1).
B. I(2;-1;0).
C. I(3; -2;1).
D. I(-3; -2;1).
Trong không gian Oxyz, cho tứ diện đều ABCD có A(0;1;2). Gọi H là hình chiếu vuông góc của A lên mặt phẳng (BCD). Cho H(4;-3;-2). Tọa độ tâm I và bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD là:
A. I(2; -1; 0); R = 2 3
B. I(4; -3; -2); R = 4 3
C. I(3; -2; -1); R = 3 3
D. I(3; -2; -1); R = 9
Đáp án C
Do ABCD là tứ diện đều nên H là trọng tâm tam giác BCD và I trùng với trọng tâm G của tứ diện ABCD. Ta có:
![]()
![]()
Từ đó ta có:
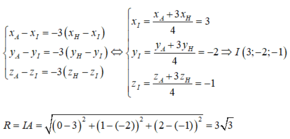
Vậy đáp án C đúng.
Trong không gian tọa độ Oxyz, cho tứ diện ABCD có A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Thể tích của tứ diện ABCD bằng
A. 1
B. 2
C. 1 2
D. 1 3
Chọn đáp án C.
Ta có
![]()
![]()
Áp dụng công thức ta có:
V A B C D = 1 6 A B ⇀ . A C ⇀ . A D ⇀ = 1 2
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có:
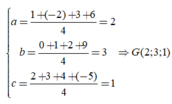
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có:
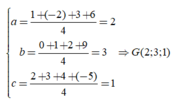
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y 2 + z − 2 2 = 9 ngoại tiếp khối bát diện (H) được ghép từ hai khối chóp tứ giác đều S.ABCD và S’.ABCD (đều có đáy là tứ giác ABCD). Biết rằng đường tròn ngoại tiếp của tứ giác ABCD là giao tuyến của mặt cầu (S) và mặt phẳng P : 2 x + 2 y − z − 8 = 0 . Tính thể tích khối bát diện (H)
A. V H = 34 9 .
B. V H = 665 81 .
C. V H = 68 9 .
D. V H = 1330 81 .
Đáp án C
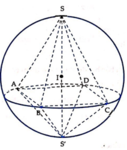
Mặt cầu (S) có tâm I 1 ; 0 ; 2 , bán kính R=3. Nhận xét thấy S, I, S’ thẳng hàng và S S ' ⊥ A B C D . Khi đó S S ' = 2 R = 6 . Ta có:
V H = V S . A B C D + V S ' . A B C D = 1 3 d S ; A B C D . S A B C D + 1 3 d S ' ; A B C D . S A B C D
= 1 3 d S ; A B C D + d S ' ; A B C D . S A B C D = 1 3 S S ' . S A B C D = 2 S A B C D
Từ giả thiết suy ra ABCD là hình vuông, gọi a là cạnh hình vuông đó.
Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng r và ngoại tiếp hình vuông ABCD.
Suy ra 2 r = A C = a 2 ⇒ r = a 2 2 . Từ d I ; P 2 + r 2 = R 2 .
⇔ r = R 2 − d I ; P 2 = 3 2 − 8 3 2 = 17 3 = a 2 2 ⇔ a = 2 17 3 2
Vậy V H = 2 S A B C D = 2 a 2 = 2. 2 17 3 2 2 = 68 9 .
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y 2 + z − 2 2 = 9 ngoại tiếp khối bát diện (H) được ghép từ hai khối chóp tứ giác đều S.ABCD và S’.ABCD (đều có đáy là tứ giác ABCD). Biết rằng đường tròn ngoại tiếp của tứ giác ABCD là giao tuyến của mặt cầu (S) và mặt phẳng P : 2 x + 2 y − z − 8 = 0 . Tính thể tích khối bát diện (H)
A. V H = 34 9 .
B. V H = 665 81 .
C. V H = 68 9 .
D. V H = 1330 81 .
Trong không gian Oxyz, cho hai mặt cầu S 1 : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z + 2 = 0 và S 2 : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z - 4 = 0 . Xét tứ diện ABCD có hai đỉnh A,B nằm trên (S1); hai đỉnh C,D nằm trên (S2 ). Thể tích khối tứ diện ABCD có giá trị lớn nhất bằng
A. 3 2
B. 2 3
C. 6 3
D. 6 2
Trong không gian Oxyz, cho hai mặt cầu ( S 1 ) : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z + 2 = 0 và ( S 2 ) : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z - 4 = 0 . Xét tứ diện ABCD có hai đỉnh A, B nằm trên S1; hai đỉnh C,D nằm trên S2. Thể tích khối tứ diện ABCD có giá trị lớn nhất bằng
A. 3 2
B. 2 3
C. 6 3
D. 6 2
Trong không gian Oxyz, cho tam giác đều ABC với A (5;3;-1) và B (2;3;-4) điểm C nằm trong mặt phẳng Oxyz có tung độ nhỏ hơn 3.
a) Tìm tọa độ điểm D biết ABCD là tứ diện đều.
b) Tìm tọa độ điểm S biết SA, SB, SC đôi một vuông góc.
Không có mặt phẳng nào là mặt phẳng Oxyz cả nên chắc đề ko đúng. Giả sử nó là Oxy đi
Ý tưởng giải bài toán như sau:
- Viết phương trình mp trung trực (P) của đoạn AB
- Viết pt tham số đường thẳng d là giao của (P) và Oxy
- C thuộc d nên quy tọa độ C về 1 ẩn
- Tính độ dài AB=AC sẽ tìm được tọa độ C
- Viết phương trình mp trung trực (Q) của AC
- Viết pt tham số đường thẳng d1 là giao của (P) và (Q)
- D thuộc d1 => quy tọa độ D theo 1 ẩn, tính độ dài AD=AB => tọa độ D
Câu b thì giải hệ 3 tích vô hướng: SA.SB, SA.SC, SB.SC=0
Chết, ghi lộn đợi mình ăn xong mình tìm lại đề nhé bạn 😁