Tìm m để tâm đối xứng của đồ thị hàm số C : y = x 3 + m + 3 x 2 + 1 − m trùng với tâm đối xứng của đồ thị hàm số H : y = 14 x − 1 x + 2 .
A. m=2
B. m=1
C. m=3
D. m=0
Cho hàm số y = x - 1 x + m , m ≠ - 1 , có đồ thị (C). Tìm m để đồ thị (C) nhận I (2;) làm tâm đối xứng.
A. m = 1 2
B. m = - 1 2
C. m = 2
D. m = -2
Chọn: D
Đồ thị (C) nhận I (2;1) làm tâm đối xứng
![]()
Tìm m để đồ thị hàm số sau nhận gốc tọa độ O làm tâm đối xứng y = x 3 − ( m 2 − 9) x 2 + (m + 3)x + m − 3.
A. m = 3
B. m = 4
C. m = 1
D. m = 2
Tìm m để đồ thị hàm số y = a x + 1 2 x - b nhận điểm I(1;1) làm tâm đối xứng
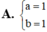
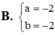
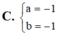
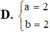
Cho hàm số y = 2x+1/x-1 (C)
Xác định tham số m để đường thẳng d : y = x +m cắt đồ thị (C) tại hai điểm phân biệt M,N sao cho diện tích tam giác IMN bằng 4 ( I là tâm đối xứng của đồ thị (C))
Tìm tất cả các giá trị của tham số m sao cho đồ thị C m của hàm số y = m x + 3 1 - x có tiệm cận và tâm đối xứng của đồ thị thuộc đường thẳng d : 2 x - y + 1 = 0
A. với mọi m
B. không có m
C. m = 3
D. m = -3
Chọn B
Điều kiện để đồ thị có tiệm cận: m ≠ - 3
Tâm đối xứng I(1;-m) là giao điểm của hai đường tiệm cận.
Khi đó, I ∈ d ⇔ m = - 3 (loại). Vậy không tồn tại m thỏa mãn.
Tìm tất cả các giá trị của tham số m sao cho đồ thị (Cm) của hàm số y = m x + 3 1 - x có tiệm cận và tâm đối xứng của đồ thị thuộc đường thẳng d:2x-y+1=0
A. với mọi m
B. không có m
C. m = 3
D. m = -3
Đáp án B
Điều kiện để đồ thị có tiệm cận: ![]()
Tâm đối xứng I(1;-m) là giao điểm của hai đường tiệm cận.
Khi đó, ![]() (loại). Vậy không tồn tại m thỏa mãn.
(loại). Vậy không tồn tại m thỏa mãn.
Cho hàm số y = x x - 1 có đồ thị (C) .Gọi ∆ là tiếp tuyến tại điểm M(x0; y0) (với x0 > 0) thuộc đồ thị (C). Để khoảng cách từ tâm đối xứng I của đồ thị (C) đến tiếp tuyến là lớn nhất thì tung độ của điểm M gần giá trị nào nhất?
A. 7 π 2
B. 3 π 2
C. 5 π 2
D. π 2
+ Hàm số đã cho có TCĐ là x=1 và TCN là y= 1 nên tâm đối xứng- là giao điểm của 2 đường tiệm cận có tọa độ là I (1; 1)
+ Ta có ![]()
Gọi 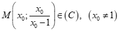
+ Phương trình tiếp tuyến tại M có dạng
![]()
![]()
+ 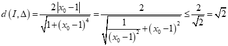
+ Dấu " = " xảy ra khi và chỉ khi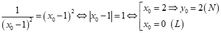
Tung độ này gần với giá trị ![]() nhất trong các đáp án.
nhất trong các đáp án.
Chọn D.
Tìm tọa độ tâm đối xứng của đồ thị hàm số y=(2x+1)/(x-1)
A. (1;2)
B. (2;1)
C. (1;-1)
D. (-1;1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số :
\(y=\dfrac{x+2}{x-3}\)
b) Chứng minh rằng giao điểm I của hai tiệm cận của (C) là tâm đối xứng của (C)
c) Tìm điểm M trên đồ thị của hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang
b) Tiệm cận đứng là đường thẳng \(x=3\)
Tiệm cận ngang là đường thẳng \(y=1\)
