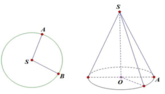
Cho hình tròn tâm S, bán kính R = 2 . Cắt đi 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón như hình vẽ. Tính diện tích toàn phần của hình nón đó.
A. 21 π 4
B. 3 + 4 3 π
C. 3 + 2 3 π
D. 3 π
Cho hình tròn tâm S, bán kính R = 2 . Cắt đi 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón như hình vẽ. Tính diện tích toàn phần của hình nón đó.
![]()
![]()
![]()
![]()
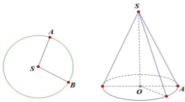
Cho hình tròn tâm S, bán kính R = 2. Cắt đi 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón. Tính diện tích toàn phần của hình nón đó.
![]()
![]()
![]()
![]()
Chọn đáp án A
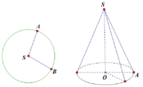
Đường tròn (S; R) có
+ Chu vi hình tròn (S; R) là C = 4 π
+ Diện tích hình tròn (S; R) là S = 4 π . Khi cắt 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón, ta có. Diện tích xung quanh hình nón là
![]()
Chu vi đáy của hình nón là
![]()
bán kính đáy của hình nón là r = 3 2
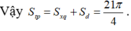
Cho hình tròn tâm S, bán kính R = 2. Cắt bỏ 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của một hình nón N. Tính diện tích toàn phần S t p của hình nón N.
![]()
![]()
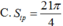
![]()
Cho hình tròn tâm S, bán kính R = 2. Cắt bỏ 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của một hình nón N. Tính diện tích toàn phần S t p của hình nón N
A. S t p = 3 π
B. S t p = π 3 + 2 3
C. S t p = 21 π 4
D. S t p = π 3 + 4 3
Cho hình tròn (C), bán kính R = 2. Cắt 1 4 hình tròn (C) (như hình vẽ), rồi lấy 1 4 hình tròn đó dán kín OA và OB lại để tạo ra mặt xung quanh của một hình nón. Tính diện tích toàn phần của hình nón.

A. S t p = 5 π
B. S t p = 5 π 2
C. S t p = 5 π 8
D. S t p = 5 π 4
Hình nón được tạo thành có độ dài đường sinh là l = OA = 2, chu vi đường tròn đáy bằng độ dài cung AB và bằng

Cho hai mặt phẳng (P) và (Q) song song với nhau cắt khối cầu tâm O bán kính R tạo thành hai hình tròn (C1) và (C2) cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn, đáy trùng với hình tròn còn lại. Biết diện tích xung quanh của hình nón là lớn nhất, khi đó thể tích khối trụ có hai đáy là hai hình tròn (C1) và (C2) bằng:
A. 4 π R 3 3 9
B. 2 π R 3 3 9
C. π R 3 3 9
D. 4 π R 3 3 3
Cho hình nón tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm.
a) Tính diện tích xung quanh của hình nón đã cho.
b) TÍnh thể tích của khối nón được tạo bởi hình nón đó.
c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12 cm. Tính diện tích thiết diện đó.
a) Đường sinh l của hình nón là:
l = =
= 5√41 (cm).
Diện tích xung quanh của hình nón là:
Sxq = πrl = 125π√41 (cm2)
b) Vnón = = (625.20π)/3 = (12500π)/3 (cm3)
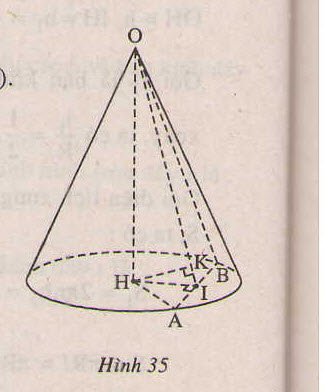
c) Giả sử thiết diện cắt hình tròn đáy theo đoạn thẳng AB.
GỌi I là trung điểm AB, O là đỉnh của nón thì thiết diện là tam giác cân OAB.
Hạ HK vuông góc AI, H là tâm của đáy, thì HK vuông góc ( OAB) và theo giả thiết HK = 12 (cm)
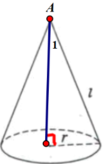
Cắt mặt xung quanh của một hình nón tròn xoay dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính R. Hỏi hình nón đó có bán kính r của đường tròn đáy và góc ở đỉnh của hình nón bằng bao nhiêu ?
Cắt mặt xung quanh của một hình nón tròn xoay dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính R ⇒ đường sinh có độ dài bằng R và chu vi đường tròn đáy bằng nửa chu vi đường tròn bán kính R
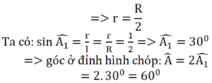
Cho hai mặt phẳng (P) và (Q) song song với nhau và cắt một mặt cầu tâm O bán kính R tạo thành hai đường tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai đường tròn và đáy trùng với đường tròn còn lại. Tính khoảng cách giữa (P) và (Q) để diện tích xung quanh hính nón đó là lớn nhất.
![]()
![]()
![]()