Hình nón được tạo thành có độ dài đường sinh là l = OA = 2, chu vi đường tròn đáy bằng độ dài cung AB và bằng

Hình nón được tạo thành có độ dài đường sinh là l = OA = 2, chu vi đường tròn đáy bằng độ dài cung AB và bằng

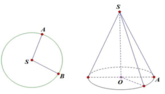
Cho hình tròn tâm S, bán kính R = 2 . Cắt đi 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón như hình vẽ. Tính diện tích toàn phần của hình nón đó.
A. 21 π 4
B. 3 + 4 3 π
C. 3 + 2 3 π
D. 3 π
Cho hình tròn tâm S, bán kính R = 2. Cắt bỏ 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của một hình nón N. Tính diện tích toàn phần S t p của hình nón N
A. S t p = 3 π
B. S t p = π 3 + 2 3
C. S t p = 21 π 4
D. S t p = π 3 + 4 3
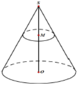
Một hình nón có chiều cao S O = 50 c m và có bán kính đáy bằng 10 c m . Lấy điểm M thuộc đoạn SO sao cho O M = 20 c m . Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn C . Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi C (xem hình vẽ).
A. 16 π 26 c m 2
B. 26 π 26 c m 2
C. 36 π 26 c m 2
D. 46 π 26 c m 2
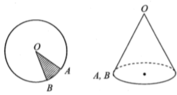
Cho một miếng tôn hình tròn tâm O, bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O không có đáy (OA trùng với OB). Gọi S và S ' lần lượt là diện tích của miếng tôn hình tròn banđầu và diện tích của miếng tôn còn lại. Tìm tỉ số S ' S để thể tích của khối nón đạt giá trị lớn nhất
A. 2 2
B. 1 4
C. 1 3
D. 6 3
Cho miếng tôn hình tròn tâm O bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O hông đáy (OA trùng với OB). Gọi S, S’ lần lượt là diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số S ' S để thể tích khối nón lớn nhất
A. 6 3
B. 1 4
C. 2 3
D. 1 3
Từ một hình tròn có tâm S, bán kính R, người ta tạo ra các hình nón theo hai cách sau đây
Cách 1: Cắt bỏ 1/4 hình nón rồi ghép hai mép lại được hình nón N 1
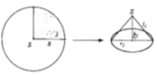
Cách 2: Cắt bỏ 1/2 hình nón rồi ghép hai mép lại được hình nón N 2
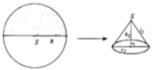
Gọi V 1 , V 2 lần lượt là thể tích của khối nón N 1 và khối nón N 2 . Tính V 1 V 2
A. V 1 V 2 = 9 3 4 2
B. V 1 V 2 = 3 3 2 2
C. V 1 V 2 = 7 2 3
D. V 1 V 2 = 9 7 8 3
Cho một miếng tôn hình tròn tâm O, bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O không có đáy (OA trùng với OB). Gọi S và S ' lần lượt là diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số S S ' để thể tích của khối nón đạt giá trị lớn nhất
A. 2 3
B. 1 4
C. 1 3
D. 6 3
Cho hình nón tròn xoay đỉnh S, đáy là một hìnht tròn tâm O bán kính R, chiều cao của hình nón bằng 2R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho IO=2R. Giả sử A là điểm trên đường tròn (O) sao cho O A ⊥ O I . Diện tích xung quanh của hình nón bằng:

A. π R 2 2
B. π R 2 3
C. π R 2 2 5
D. π R 2 5
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (N) và hình nón (T).
A. V T V N = 2 6
B. V T V N = 2 3
C. V T V N = 3 2
D. Đáp án khác