Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc B A D ^ = 120 ° . Cạnh bên SA vuông góc với đáy (ABCD) và SA = 3a. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.BCD
A. 3 a 3
B. 5 a 3
C. 5 a 3
D. 4 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 120 ° . Cạnh bên S A = 3 a và SA vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.BCD.
A. V = a 3 2
B. V = a 3 4
C. V = 3 a 3 4
D. V = 3 a 3 2
Đáp án B
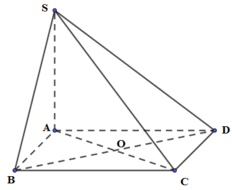
Phương pháp:
Thể tích khối chóp: V = Sh
Cách giải:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 120 0 .Cạnh bên S A = 3 a và SA vuông góc với (ABCD) .Tính a theo Vcủa khối chóp S.ABCD?
A. V = a 3 2
B. V = a 3 4
C. V = 3 a 3 4
D. V = 3 a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , A B C ⏞ = 60 0 , cạnh bên SA vuông góc với đáy SA= a 3 Tính thể tích của khối chóp S.ABCD
A. a 3 4 .
B. a 3 3 6
C. a 3 2
D. a 3 3 3
Đáp án là C.
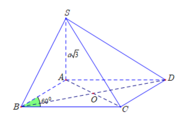
Ta có: S A B C = 1 2 B A . B C . sin A B C ⏞ = 1 2 a . a . sin 60 0 = a 2 3 4 ⇒ S A B C D = 2 S A B C = a 2 3 2 .
Thể tích của khối chóp S.BCD là:
V S . B C D = 1 3 S A . S B C D = 1 3 S A . 1 2 S A B C D = 1 3 . A = a 3 . a 2 3 2 = a 8 2 .
Cho hình chóp S.ABCD có SC ⊥ (ABCD), đáy ABCD là hình thoi có cạnh bằng a 3 v à B C D ^ = 120 ° . Biết rằng góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45°. Tính theo a thể tích khối chop S.ABCD.
A. 3 a 3 12
B. 3 3 a 3 2
C. 3 a 3 4
D. 3 3 a 3 4
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Cạnh bên SA vuông góc với đáy (ABCD) và SA=3a. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABCD
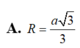
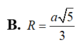
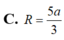
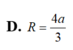
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa mặt bên hình chóp S.ABCD và mặt phẳng đáy có tang bằng:
A. 1
B. 3
C. 3 2
D. Đáp án khác
Cho hình chóp S.ABCD có có đáy là hình thoi cạnh a, góc ABC = 120 độ, SA vuông góc với (ABCD). Biết góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 độ. K là trung điểm của SC tính d(BK;AD)
Dễ dàng chứng minh \(BD\perp\left(SAC\right)\Rightarrow BD\perp SC\)
Gọi O là tâm đáy, kẻ \(OH\perp SC\Rightarrow SC\perp\left(BDH\right)\)
\(\Rightarrow\widehat{BHD}\) hoặc góc bù của nó là góc giữa (SBC) và (SCD) \(\Rightarrow\widehat{BHD}=60^0\) hoặc \(120^0\)
\(\Rightarrow\widehat{BHO}\) bằng \(30^0\) hoặc \(60^0\)
Tam giác ABD đều \(\Rightarrow BD=a\) \(\Rightarrow OB=\dfrac{a}{2}\)
TH1: \(\widehat{BHO}=30^0\)
\(\Rightarrow OH=\dfrac{OB}{tan30^0}=\dfrac{a\sqrt{3}}{2}=OC\Rightarrow\Delta\) vuông OCH có cạnh huyền bằng cạnh góc vuông (loại)
TH2: \(\widehat{BHO}=60^0\Rightarrow OH=\dfrac{OB}{tan60^0}=\dfrac{a\sqrt{3}}{6}\)
\(\Rightarrow SA=AC.tan\widehat{SCA}=AC.\dfrac{OH}{\sqrt{OC^2-OH^2}}=\dfrac{a\sqrt{6}}{4}\)
Từ A kẻ \(AM\perp SB\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM=d\left(A;\left(SBC\right)\right)\)
\(AD||BC\Rightarrow AD||\left(SBC\right)\Rightarrow d\left(BK;AD\right)=d\left(AD;\left(SBC\right)\right)=d\left(A;\left(SBC\right)\right)=AM\)
\(\dfrac{1}{AM^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{11}{3a^2}\Rightarrow AM=\dfrac{a\sqrt{33}}{11}\)
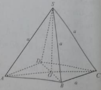
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa hai mặt bên hình chóp S.ABCD và mặt phẳng đáy có tan bằng:
A. 1
B. 3
C. 3 2
D. 2 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Cạnh bên SA vuông góc với đáy, \(\widehat{BAD}=120^0\). M là trung đierm của cạnh BC và \(\widehat{SMA=45^0}\). Tính thể tích khối chóp S.ABCD và tính khoảng cách từ D đến mặt phẳng (SBC) theo a
\(\widehat{BAD}=120^0\Rightarrow\widehat{ABC}\Rightarrow\Delta ABC\) đều
\(\Rightarrow AM=\frac{a\sqrt{3}}{2}\Rightarrow S_{ABCD}=\frac{a^3\sqrt{3}}{2}\)
Tam giác SAM vuông tại A có \(\widehat{SMA}=45^0\Rightarrow\) Tam giác SAM vuông tại A : SA = AM = \(\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABCD}=\frac{1}{3}SA.S_{ABCD}=\frac{a^3}{4}\)
Do AD song song với BC nên d(D;(SBC))=d(A,(SBC))
Gọi H là hình chiếu vuông góc của A trên SM
Ta có : \(\begin{cases}AM\perp BC\\SA\perp BC\end{cases}\)\(\Rightarrow BC\perp\cdot\left(SAM\right)\)
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A,\left(SBC\right)\right)=AH\)
Ta có :
\(AH=\frac{AM\sqrt{2}}{2}=\frac{a\sqrt{6}}{4}\Rightarrow d\left(D,\left(SBC\right)\right)=\frac{a\sqrt{6}}{4}\)