nhờ cô giúp em phép chia này với ạ : 327:3

Những câu hỏi liên quan
Em xin phép nhờ quý thầy cô hỗ trợ giúp em bài này với ạ
Tổng của các số tròn chục nhỏ hơn 90
CÁc số tròn chục nhỏ hơn 90 là :
10 ; 20 ; 30 ; 40 ; 50 ; 60 ; 70 ; 80
Tổng của các số tròn chục nhỏ hơn 90 là :
10 + 20 + ... + 80 = ( 80 + 10 ) x 8 : 2
= 90 x 8 : 2 = 720 : 2 = 360
Em xin phép nhờ quý thầy cô hỗ trợ cho em bài này với ạ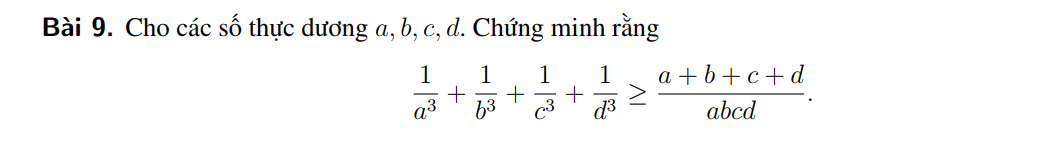
Thực hiện lần lượt BĐT cô-si 3 số cho từng bộ 3 vế trái, ví dụ:
\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\ge3\sqrt[3]{\dfrac{1}{a^3b^3c^3}}=\dfrac{3}{abc}\)
Làm tương tự, sau đó cộng vế và quy đồng vế phải là sẽ được BĐT cần chứng minh
Đúng 1
Bình luận (0)
Xin phép nhờ quý thầy cô giúp đỡ em với ạ!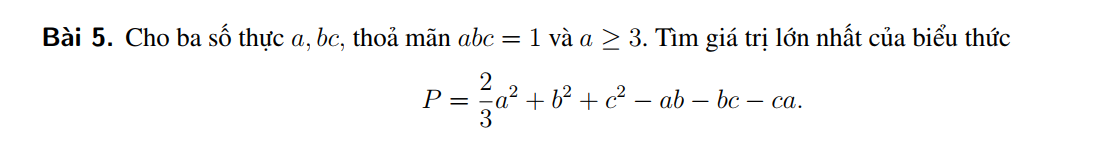
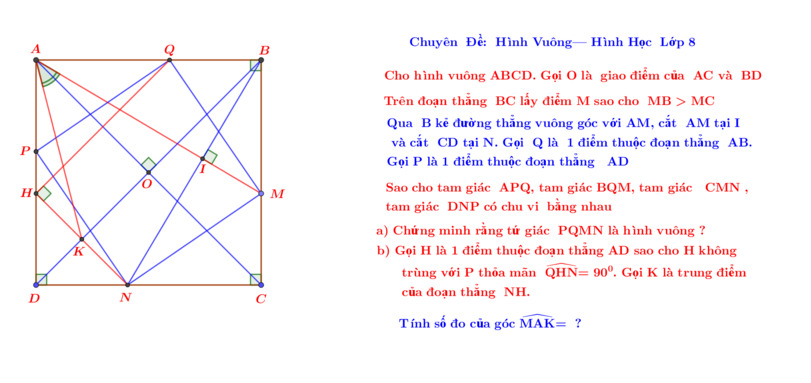
Em xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ, em cám ơn nhiều ạ
-Để mình suy nghĩ ngồi làm cho bạn nhé.
Đúng 0
Bình luận (0)
-Vì bài dài quá nên mình nói tóm tắt:
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......
Đúng 0
Bình luận (1)
Em xin phép nhờ thầy cô và các bạn giúp đỡ với ạ, em cám ơn nhiều
nhờ thầy cô giúp em giải bài 8 này với ạ
Bài 7:
a. \(x+\dfrac{2}{5}=\dfrac{6}{7}\)
\(x=\dfrac{6}{7}-\dfrac{2}{5}=\dfrac{16}{35}\)
b. \(x=6,3.1,5=9,45\)
Câu 8:
Đáy bé là: \(\dfrac{2}{3}.120=80\) m
Diện tích thửa ruộng là:
( 120 + 80) x 76 : 2 = 7600 m vuông
Số kg thu hoạch được là:
7600 : 100 x 64,5 = 4902 kg
Đổi 4902 kg = 49,02 tạ thóc
Đúng 3
Bình luận (0)
Xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ. Em cám ơn nhiều
Cho hai số nguyên \(a;b\) thỏa mãn điều kiện \(a^2+b^2\) chia hết cho 7.
Chứng minh rằng \(a;b\) đều chia hết cho 7.
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý, giúp đỡ em với ạ!
Em cám ơn nhiều ạ!
Nhận xét: với mọi n nguyên thì \(n^2\equiv\left\{0;1;2;4\right\}\left(mod7\right)\)
Giả sử a;b tồn tại 1 số không chia hết cho 7
\(\Rightarrow a^2+b^2\equiv\left\{1;2;3;4;5;6;8\right\}\left(mod7\right)\)
\(\Rightarrow a^2+b^2\) luôn ko chia hết cho 7 (trái với giả thiết)
Vậy điều giả sử là sai hay \(a;b\) đều chia hết cho 7
Đúng 2
Bình luận (0)
Chứng minh rằng với mọi số nguyên dương \(n\) thì số \(A=59^n-17^n-9^n+2^n\) chia hết cho 35.
P/s: Em xin phép nhờ sự giúp đỡ của quý thầy cô giáo và các bạn yêu toán với ạ!
Em cám ơn nhiều lắm ạ!
Ta có: \(59\equiv3\left(mod7\right)\Rightarrow59^n\equiv3^n\left(mod7\right)\)
Tương tự: \(17^n\equiv3^n\left(mod7\right)\) ; \(9^n\equiv2^n\left(mod7\right)\)
\(\Rightarrow A\equiv3^n-3^n-2^n+2^n\left(mod7\right)\)
\(\Rightarrow A⋮7\)
Vẫn tương tự, ta có: \(A\equiv4^n-2^n-4^n+2^n\left(mod5\right)\)
\(\Rightarrow A⋮5\)
Mà 7 và 5 nguyên tố cùng nhau
\(\Rightarrow A⋮35\)
Đúng 1
Bình luận (0)









