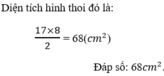Tính diện tích hình thoi có cạnh là 17cm và tổng hai đường chéo là 46cm

Những câu hỏi liên quan
Tính diện tích hình thoi có cạnh là 17cm và tổng hai đường chéo là 46cm.
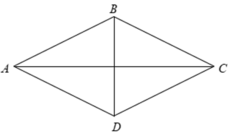
Gọi H là giao điểm của hai đường chéo AC,BD.
Theo giải thiết ta có: AC + BD = 46( cm )
⇔ ( HB + HD ) + ( HC + HA ) = 46
⇔ 2HB + 2HA = 46 ⇔ HA + HB = 23
Khi đó ta có

Đúng 0
Bình luận (0)
tính diện tích hình thoi có cạnh là 17cm, tổng hai đường chéo bằng 46cm
tính diện tích hình thoi có cạnh bằng 17cm, tổng hai đường chéo bằng 46cm
giúp mình nhé cảm ơn bạn nhiều !
gọi O là giao điểm của hai đường chéo AC và BD
Đặt OA=x,OB=y,ta có x+y=23 và x^2+y^2=17^2=289
Diện tích hình thoi ABCD=1/2 (AC.BD )=1/2 ( 2x.2y) =2xy
Từ x+y =23 mà (x+y)^2 =529
suy ra x^2 +2xy+y^2 =529
2xy+289=529
2xy =240
Vậy diện tích hình thoi ABCD là 240 cm^2
Đúng 0
Bình luận (0)
diện tích tam giác là :
23 . 23 : 2 = 264 . 5 ( cm2)
đáp số : ..................................
Đúng 0
Bình luận (0)
Gọi H là giao điểm của hai đường chéo AC,BD.
Theo giải thiết ta có: AC + BD = 46( cm )
⇔ ( HB + HD ) + ( HC + HA ) = 46
⇔ 2HB + 2HA = 46 ⇔ HA + HB = 23
Khi đó ta có: HA + HB = 23

Đúng 0
Bình luận (0)
Tính diện tích hình thoi có cạnh bằng 17cm, tổng hai đường chéo bằng 46 cm.
Đặt OA = x và OB =y, ta có:
S A B C D = 1 2 A C . B D = 1 2 2 x .2 y = 2 x y
Theo giả thiết, ta có: 2 ( x + y ) = 46 x 2 + y 2 = 17 2 = 289
Þ 2xy =240 Þ SABCD = 240cm2
Đúng 0
Bình luận (0)
Một hình thoi có độ dài hai đường chéo là 17cm và 32cm. Diện tích của hình thoi là: A . 272
cm
2
B . 270
cm
2
C . 725
cm
2
D .277
cm
2
Đọc tiếp
Một hình thoi có độ dài hai đường chéo là 17cm và 32cm. Diện tích của hình thoi là:
A . 272 cm 2
B . 270 cm 2
C . 725 cm 2
D .277 cm 2
Một hình thoi có độ dài hai đường chéo là 17cm và 32cm. Diện tích của hình thoi là: A. 272
cm
2
B . 270
cm
2
C . 725
cm
2
D.277
cm
2
Đọc tiếp
Một hình thoi có độ dài hai đường chéo là 17cm và 32cm. Diện tích của hình thoi là:
A. 272 cm 2
B . 270 cm 2
C . 725 cm 2
D.277 cm 2
Một hình thoi có độ dài hai đường chéo là 42cm và 17cm. Diện tích của hình thoi là:
Diện tích hình thoi là:
\(42\cdot\dfrac{17}{2}=21\cdot17=357\left(cm^2\right)\)
Đúng 1
Bình luận (0)
bài giải :
diện tích hình thoi là :
42 x 17 : 2 = 375 ( cm2 )
đáp số : 375 cm2.
chúc bạn học tốt nhé ^^
Đúng 0
Bình luận (0)
Một hình thoi có độ dài hai đường chéo là 17cm và 32 cm. Diện tích của hình thoi là A.
272
c
m
2
B.
270
c
m
2
C.
725
c
m
2
D.
277
c
m
2
Đọc tiếp
Một hình thoi có độ dài hai đường chéo là 17cm và 32 cm. Diện tích của hình thoi là
A. 272 c m 2
B. 270 c m 2
C. 725 c m 2
D. 277 c m 2
Diện tích hình thoi có độ dài hai đường chéo là 17cm và 8cm là: A. 25
c
m
2
B. 50
c
m
2
C. 68
c
m
2
D. 136
c
m
2
Đọc tiếp
Diện tích hình thoi có độ dài hai đường chéo là 17cm và 8cm là:
A. 25 c m 2
B. 50 c m 2
C. 68 c m 2
D. 136 c m 2