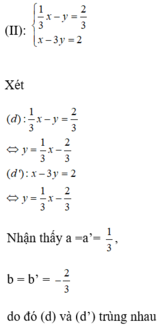Đoán nhận số nghiệm của hệ phương trình sau bằng hình học: 2 x - y = 1 x - 2 y = - 1

Những câu hỏi liên quan
Đoán nhận số nghiệm của hệ phương trình sau bằng hình học: 2 x + y = 4 - x + y = 1
Xét (II): 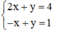
Ta biểu diễn hai đường thẳng (d): 2x + y = 4 và (d’): -x + y = 1 trên mặt phẳng tọa độ.
+ Xét (d): 2x + y = 4 hay (d): y = -2x + 4
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
+ Xét (d’) : -x + y = 1 hay (d’) : y = x + 1.
Chọn x = 0 ⇒ y = 1
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm (0; 1) và (-1; 0).
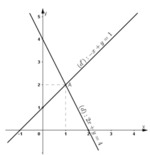
Nhận thấy (d) và (d’) cắt nhau tại A (1; 2).
Thử lại , thay x =1, y=2 vào các phương trình của hệ (II) ta được:
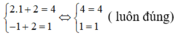
Vậy hệ phương trình (II) có đúng một nghiệm là (1; 2).
Đúng 0
Bình luận (0)
Đoán nhận số nghiệm của hệ phương trình sau bằng hình học:
a
)
2
x
−
y
1
x
−
2
y...
Đọc tiếp
Đoán nhận số nghiệm của hệ phương trình sau bằng hình học:
a ) 2 x − y = 1 x − 2 y = − 1 b ) 2 x + y = 4 − x + y = 1
a) Xét hệ (I): 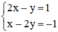
Ta biểu diễn hai đường thẳng (d): 2x – y = 1 và (d’): x – 2y = -1 trên mặt phẳng tọa độ.
+ Xét đường thẳng (d): 2x – y = 1 hay (d) : y = 2x – 1
Chọn x = 0 ⇒ y = -1.
Chọn y = 0 ⇒ x = 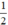
⇒ (d) đi qua hai điểm (0; -1) và 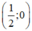
+ Xét (d’) : x – 2y = -1 hay (d’): 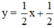
Chọn x = 0 ⇒ y = 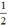
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm 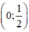 và (-1; 0).
và (-1; 0).
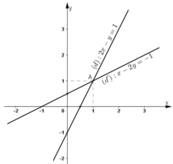
Dựa vào đồ thị thấy hai đường thẳng (d) và (d’) cắt nhau tại A (1; 1).
Thử lại, thay x =1, y=1 vào các phương trình của hệ (I) ta được:
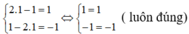
Vậy hệ phương trình (I) có một nghiệm là (1; 1)
b) Xét (II): 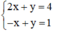
Ta biểu diễn hai đường thẳng (d): 2x + y = 4 và (d’): -x + y = 1 trên mặt phẳng tọa độ.
+ Xét (d): 2x + y = 4 hay (d): y = -2x + 4
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
+ Xét (d’) : -x + y = 1 hay (d’) : y = x + 1.
Chọn x = 0 ⇒ y = 1
Chọn y = 0 ⇒ x = -1.
⇒ (d’) đi qua hai điểm (0; 1) và (-1; 0).
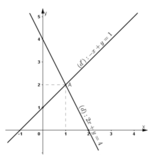
Nhận thấy (d) và (d’) cắt nhau tại A (1; 2).
Thử lại , thay x =1, y=2 vào các phương trình của hệ (II) ta được:
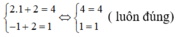
Vậy hệ phương trình (II) có đúng một nghiệm là (1; 2).
Đúng 0
Bình luận (0)
Cho các hệ phương trình sau:
x
2
2
x
-
y
3
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.
Đọc tiếp
Cho các hệ phương trình sau: x = 2 2 x - y = 3
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.
x = 2 2 x - y = 3
Đường thẳng (d): x = 2 song song với trục tung.
Đường thẳng (d’): 2x – y = 3 không song song với trục tung
⇒ (d) cắt (d’)
⇒ Hệ có nghiệm duy nhất.
Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.
Vẽ (d’): 2x - y = 3
- Cho x = 0 ⇒ y = -3 được điểm (0; -3).
- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).
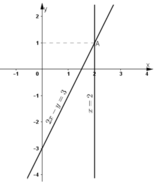
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).
Đúng 0
Bình luận (0)
Cho các hệ phương trình sau:
a
)
x
2
2
x
−
y
3
b...
Đọc tiếp
Cho các hệ phương trình sau:
a ) x = 2 2 x − y = 3 b ) x + 3 y = 2 2 y = 4
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.
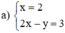
Đường thẳng (d): x = 2 song song với trục tung.
Đường thẳng (d’): 2x – y = 3 không song song với trục tung
⇒ (d) cắt (d’)
⇒ Hệ có nghiệm duy nhất.
Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.
Vẽ (d’): 2x - y = 3
- Cho x = 0 ⇒ y = -3 được điểm (0; -3).
- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).
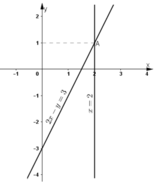
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).
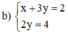
Đường thẳng (d): x + 3y = 2 không song song với trục hoành
Đường thẳng (d’): 2y = 4 hay y = 2 song song với trục hoành
⇒ (d) cắt (d’)
⇒ Hệ phương trình có nghiệm duy nhất.
Vẽ (d1): x + 3y = 2
- Cho y = 0 ⇒ x = 2 được điểm (2; 0).
- Cho x = 0 ⇒ y = 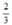 được điểm (0;
được điểm (0; 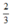 ).
).
Vẽ (d2): y = 2 là đường thẳng đi qua (0; 2) và song song với trục hoành.
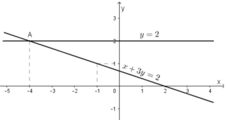
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(-4; 2).
Vậy hệ phương trình có nghiệm (-4; 2).
Đúng 0
Bình luận (0)
Cho các hệ phương trình sau:
x
+
3
y
2
2
y
4
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách...
Đọc tiếp
Cho các hệ phương trình sau: x + 3 y = 2 2 y = 4
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.
x + 3 y = 2 2 y = 4
Đường thẳng (d): x + 3y = 2 không song song với trục hoành
Đường thẳng (d’): 2y = 4 hay y = 2 song song với trục hoành
⇒ (d) cắt (d’)
⇒ Hệ phương trình có nghiệm duy nhất.
Vẽ (d1): x + 3y = 2
- Cho y = 0 ⇒ x = 2 được điểm (2; 0).
- Cho x = 0 ⇒ y = 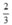 được điểm (0;
được điểm (0; 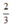 ).
).
Vẽ (d2): y = 2 là đường thẳng đi qua (0; 2) và song song với trục hoành.
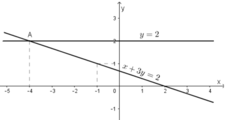
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(-4; 2).
Vậy hệ phương trình có nghiệm (-4; 2).
Đúng 0
Bình luận (0)
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao: x + y = 2 3 x + 3 y = 2
(I): 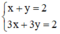
Xét (d): x + y = 2 hay (d): y = -x + 2 có a = -1; b = 2.
(d’) 3x + 3y = 2 hay (d’): y = -x + 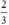 có a’ = -1 ; b’ =
có a’ = -1 ; b’ = 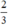
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (I) vô nghiệm.
Đúng 0
Bình luận (0)
Bài 5 (trang 11 SGK Toán 9 Tập 2): Đoán nhận số nghiệm của hệ phương trình sau bằng hình học:
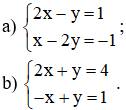
Nhớ lập bảng giá trị cho mình xem nhé
a: \(\left\{{}\begin{matrix}2x-y=1\\x-2y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x-1\\2y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2x-1\\y=\dfrac{1}{2}x+1\end{matrix}\right.\)
Vì \(2< >\dfrac{1}{2}\)
nên hai đường thẳng y=2x-1 và y=1/2x+1 sẽ cắt nhau tại 1 điểm duy nhất
=>Hệ sẽ có 1 nghiệm
b: \(\left\{{}\begin{matrix}2x+y=4\\-x+y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-2x+4\\y=x+1\end{matrix}\right.\)
Vì -2<>1 nên hai đường thẳng y=-2x+4 và y=x+1 sẽ cắt nhau tại 1 điểm duy nhất
=>Hệ sẽ có 1 nghiệm duy nhất
Đúng 0
Bình luận (0)
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
1
3
x
-
y
2
3
x
-
3
y...
Đọc tiếp
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
1 3 x - y = 2 3 x - 3 y = 2
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a
)
x
+
y
2
3
x
+
3
y...
Đọc tiếp
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a ) x + y = 2 3 x + 3 y = 2 b ) 3 x − 2 y = 1 − 6 x + 4 y = 0
a) (I): 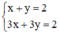
Xét (d): x + y = 2 hay (d): y = -x + 2 có a = -1; b = 2.
(d’) 3x + 3y = 2 hay (d’): y = -x + 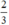 có a’ = -1 ; b’ =
có a’ = -1 ; b’ = 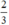
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (I) vô nghiệm.
b) (II): 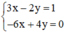
Xét: (d): 3x – 2y = 1 hay (d):
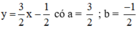
(d’): -6x + 4y = 0 hay (d’):
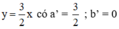
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (II) vô nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 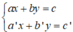
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.
Đúng 0
Bình luận (0)