Biểu diễn trên đường tròn lượng giác góc (cung) có số đo α:
a) α = 10350
b) α = 195π/3
c) α = π/2 + kπ, k∈Z
d) α = kπ
Cho góc lượng giác (Ou,Ov) có số đo là \( - \frac{{11\pi }}{4}\), góc lượng giác (Ou,Ow) có số đó là \(\frac{{3\pi }}{4}\). Tìm số đo của góc lượng giác (Ov,Ow).
Theo hệ thức Chasles, ta có:
\(\begin{array}{l}(Ov,Ow) = (Ou,Ov) - (Ou,Ow) + k2\pi \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \, - \frac{{11\pi }}{4} - \frac{{3\pi }}{4} + k2\pi = - \frac{7}{2} + k2\pi ,\,\,(k \in \mathbb{Z})\end{array}\)
Cho góc lượng giác ( OA; OB) có số đo bằng π/5. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác ( OA; O B) ?
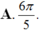
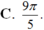
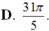
Góc lượng giác có số đo α (rad) thì mọi góc lượng giác cùng tia đầu và tia cuối với nó có số đo dạng :
A. α + k.1800 ( k là số nguyên)
B. α + k. 3600 (k là số nguyên).
C. α + k2π ( k là số nguyên).
D. α + kπ ( k là số nguyên).
Chọn C.
Nếu một góc lượng giác (Ou; Ov) có số đo α radian thì mọi góc lượng giác cùng tia đầu Ou, tia cuối Ov có số đo α + 2kπ, k ∈ Z, mỗi góc tương ứng với một giá trị của k.
Các cung lượng giác tương ứng trên đường tròn định hướng tâm O cũng có tính chất như vậy.
Tính các giá trị lượng giác của góc α, biết
cotα = 4tanα khi π/2 < α < π
Với π/2 < α < π thì sinα > 0, cosα < 0, tanα < 0
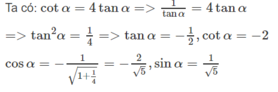
Cho góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{4\pi }}{3}\). Cho góc lượng giác \((O'u',O'v')\) có tia đầu \(O'u' \equiv Ou\), tia cuối \(O'v' \equiv Ov\). Viết công thức biểu thị số đo góc lượng giác \((O'u',O'v')\)
Ta có:
\((O'u',O'v') = (Ou,Ov) + k2\pi \,\, = \, - \frac{{4\pi }}{3}\, + k2\pi \,\,\,\,\,\,\,\,(k \in \mathbb{Z})\)
Cho ba tia Ou, Ov, Owvới số đo của các góc hình học uOv và vOw lần lượt là \({30^ \circ }\) và \({45^ \circ }\)
a) Xác định số đo của ba góc lượng giác \((Ou,Ov)\) ,\((Ov,Ow\) và \((Ou,Ow)\) được chỉ ra ở Hình 1.5.
b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để
sđ\((Ou,Ov)\) + sđ\((Ov,Ow\) = sđ \((Ou,Ow)\) + k\({.360^ \circ }\)
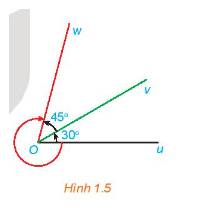
a) Ta có:
- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là
sđ\((Ou,Ov) = {30^ \circ } + n{.360^ \circ }\)
- Các góc lượng giác tia đầu Ov, tia cuối Ow có số đo là
sđ \((Ov,Ow) = {45^ \circ } + m{.360^ \circ }\)
- Các góc lượng giác tia đầu Ou, tia cuối Ow có số đo là
sđ \((Ou,Ow) = {75^ \circ } + k{.360^ \circ }\)
b) Với các góc lượng giác ở câu a, ta có:
\(sđ(Ou,Ov) +sđ (Ov,Ow)\)
\( = {30^ \circ } + n{.360^ \circ } + {45^ \circ } + m{.360^ \circ } \)
\(= {75^ \circ } + (n+m){.360^ \circ } \)
\(= {75^ \circ } + k{.360^ \circ = sđ (Ou,Ow)} \)
với k = n + m
Tính các giá trị lượng giác của góc α, biết
cosα = 2sinα khi 0 < α < π/2
Với 0 < α < π/2 thì cosα >0, sinα >0. Ta có
1 - sin 2 α = cos 2 α
Mặt khác cos 2 α = ( 2 sin α ) 2 = 4 sin 2 α nên 5 sin 2 α = 1 hay
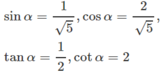
tìm góc lượng giác (Ou,Ov) có số đo dương nhỏ nhất , biết một góc lượng giác (Ou,Ov) có số đo : a) -90o ; b) 1000o ; c) \(\frac{30\pi}{7}\) ; d) -\(\frac{15\pi}{11}\)
