Cho hàm số 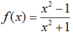 . Tập nghiệm của phương trình f’(x) = 0 là
. Tập nghiệm của phương trình f’(x) = 0 là
A. {0}
B. 0
C. 4
D. -2
hàm số \(f(x) = {x^2}{e^{ - 2x}}\). Tập nghiệm của phương trình \(f'(x) = 0\) là
A. \(\{ 0;1\} \).
B. \(\{ - 1;0\} \)
C. \(\{ 0\} \).
D. \(\{ 1\} \).
\(f'\left(x\right)=\left(x^2e^{-2x}\right)'=2x\cdot e^{-2x}-2x^2e^{-2x}\\ f'\left(x\right)=0\\ \Rightarrow2xe^{-2x}-2x^2e^{-2x}=0\\ \Leftrightarrow2xe^{-2x}\cdot\left(1-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Câu 3. Phương trình vô nghiệm có tập nghiệm là?
A. S = f B. S = 0 C. S = {0} D. S = {f}
Câu 4. Điều kiện xác định của phương trình là?
A. x ≠ 2 và B. x ≠ -2 và C. x ≠ -2 và x ≠ 3 D. x ≠ 2 và
Câu 5. Cho AB = 3cm, CD = 40cm. Tỉ số của hai đoạn thẳng AB và CD bằng?
A. B. C. D.
Cho hàm số f(x) = 5(x + 1)3 + 4(x + 1). Tập nghiệm của phương trình f ”(x) = 0 là
A. [-1 ; 2] .
B. -1.
C. {-1}.
D. ∅.
Chọn C.
Vì: f’(x) = 15(x + 1)2 + 4 ;
f”(x) = 30(x + 1) ⇔ f”(x) = 0 ⇔ x = -1.
Cho hàm số f ( x ) = 5 ( x + 1 ) 3 + 4 ( x + 1 ) . Tập nghiệm của phương trình f ' ' ( x ) = 0 là
A. [-1;2]
B. ( - ∞ ; 0 ]
C. {1}
D. ∅
Đáp án C
Ta có : f ' ( x ) = 15 ( x + 1 ) 2 + 4 ;
f ' ' ( x ) = 30 ( x + 1 ) ⇒ f ' ' ( x ) = 0 ⇔ 30 ( x + 1 ) = 0 ⇔ x = - 1 .
Cho hàm số \(f(x) = \frac{1}{3}{x^3} - {x^2} - 3x + 1\). Tập nghiệm của bất phương trình \(f'(x) \le 0\) là
A. [1 ; 3].
B. \([ - 1;3]\).
C. \([ - 3;1]\).
D. \([ - 3; - 1]\)
Ta có: \(f'\left(x\right)=x^2-2x-3\)
\(f'\left(x\right)\le0\\ \Rightarrow x^2-2x-3\le0\\ \Leftrightarrow\left(x+1\right)\left(x-3\right)\le0\\ \Leftrightarrow-1\le x\le3\)
Cho hàm số f(x)=-1/3x3 + 4x2-7x+2. Tập nghiệm của bất phương trình: f ' ( x ) ≥ 0 là
![]()
![]()
![]()
![]()
Cho hàm số 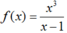 . Tập nghiệm của phương trình f’(x) = 0 là
. Tập nghiệm của phương trình f’(x) = 0 là
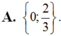
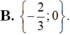


Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8
Cho hàm số 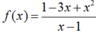 . Tập nghiệm của bất phương trình f’(x) > 0 là
. Tập nghiệm của bất phương trình f’(x) > 0 là
A. R \ {1}.
B. ∅.
C. (1; +∞).
D. R.