Cho hình chữ nhật ABCD và số thực k> 0. Tập hợp các điểm M thỏa mãn đẳng thức M A → + M B → + M C → + M D → = k
A. một đoạn thẳng.
B. một đường thẳng
C. một đường tròn.
D. một điểm
Cho hình chữ nhật ABCD và số thực k >0. Tập hợp các điểm M thỏa mãn đẳng thức M A → + M B → + M C → + M D → = k là
A. một đoạn thẳng.
B. một đường thẳng.
C. một đường tròn.
D. một điểm.
Cho hình chữ nhật ABCD và số thực k>0.Tập hợp các điểm M thỏa mãn đẳng thức :
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\right|=k\)
Gọi O là tâm hình chữ nhật
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\right|=k\)
\(\Leftrightarrow\left|\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}\right|=k\)
\(\Leftrightarrow4\left|\overrightarrow{MO}\right|=k\)
\(\Rightarrow\left|\overrightarrow{MO}\right|=\frac{k}{4}\Rightarrow\) M thuộc đường tròn tâm O bán kính \(\frac{k}{4}\)
Câu 1: Cho 2 điểm A,B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức \(\left|2.vectoMA+vectoMB\right|=\left|vectoMA+2.vectoMB\right|\)là:
A. đường trung trực của đoạn AB
B. đường tròn đường kính AB
C. đường trung trực đoạn thẳng IA
D. đường tròn tâm A, bán kính AB
Câu 2: cho tam giác ABC đều cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng thức \(\left|3.vectoMA+3.vectoMB+4.vectoMC\right|=\left|vectoMB-vectoMA\right|\)là đường tròn cố định có bán kính R. Tính bán kính R theo a.
A. R = a/3
B. R = a/9
C. R = a/2
D. R = a/6
Câu 3: Cho hình chữ nhật ABCD và số thực K>0. Tập hợp các điểm M thỏa mãn đẳng thức \(\left|vectoMA+vectoMB+vectoMC+vectoMD\right|=k\)là:
A. một đoạn thẳng
B. một đường thẳng
C. một đường tròn
D. một điểm
Câu 4:Cho tam giác ABC. Có bao nhiêu điểm M thỏa mãn \(\left|vectoMA+vectoMB+vectoMC\right|=3\)?
A.1
B.2
C.3
D. vô số
Cho hình bình hành ABCD. Tập hợp tất cả các điểm M thỏa mãn đẳng thức M A → + M B → − M C → = M D → là
A. một đường tròn.
B. một đường thẳng.
C. tập rỗng.
D. một đoạn thẳng.
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số
cho hình chữ nhật ABCD tập hợp các điểm M thỏa mãn \(\overrightarrow{|MA}+\overrightarrow{MB}|=|\overrightarrow{MC}+\overrightarrow{MD}|\)
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 ; e 2 y = 1 . Số phần tử của S là:/
A. 0
B. 1
C. 2
D. Vô số
Chọn B
Cách giải: Ta có:
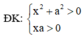
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
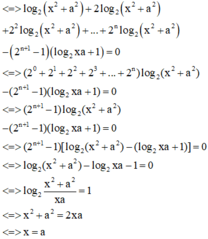
![]()
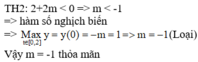
Câu 1: Cho 3 điểm A, B, C không thẳng hàng và điểm M thỏa mãn đẳng thức vecto \(\overrightarrow{MA}\)=x\(\overrightarrow{MB}\)+y\(\overrightarrow{MC}\)
Tính giá trị biểu thức P=x+y
A. P=0
B. P=2
C. P=-2
D. P=3
Câu 2: Cho hình chữ nhật ABCD và số thực k>0. Tập hợp các điểm M thỏa mãn đẳng thức \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\right|\)=k là
A. một đoạn thẳng
B. một đường thẳng
C. một đường tròn
D. một điểm
Cho tứ diện ABCD có O là trung điểm của đoạn thẳng nối trung điểm của hai cạnh đối diện và a là số thực dương không đổi. Tập hợp các điểm M trong không gian thỏa mãn hệ thức M A → + M B → + M C → + M D → = a là
A. mặt cầu tâm O bán kính r = a 3 .
B. mặt cầu tâm O bán kính r = a 4 .
C. mặt cầu tâm O bán kính r = a .
D. mặt cầu tâm O bán kính r = a 2 .
Đáp án B
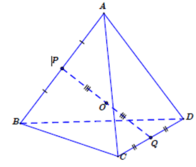
* Gọi P, Q lần lượt là trung điểm của AB, CD. Theo giả thiết O là trung điểm của PQ nên suy ra O là trọng tâm của tứ diện ABCD.
M A → + M B → + M C → + M D → = a
⇔ 4 O M → = a ⇔ O M = a 4
Vậy tập hợp các điểm M trong không gian là mặt cầu tâm O bán kính r = a 4