Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox?
![]()
![]()
![]()
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox?
A.(1; 0)
B. (0; 1)
C.(1; 1)
D.Tất cả sai
Đáp án A
Trục Ox có phương trình là y= 0.
Nên đường thẳng này có 1 VTPT là: n → ( 0 ; 1 )
Do đó 1 VTCP của đường thẳng là (1; 0)
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Oy?
A. (1; 0)
B.(0; -1)
C. (1; 1)
D. (-1; 1)
Đáp án B
Trục Oy có phương trình là x = 0.
Nên đường thẳng này có 1 VTPT là n → ( 1 ; 0 )
Do đó:1 VTCP của đường thẳng là (0; 1)
Mà 2 vectơ (0; 1) và (0; -1) là 2 vectơ cùng phương nên vectơ (0; -1) cũng là VTCP đối với trục Oy.
Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Ox?
A. (0; 1)
B. (1; 0)
C. (-1; 1)
D. (1; 1)
Đáp án A
Trục Ox có phương trình đường thẳng là y = 0. Đường thẳng này có VTPT là (0; 1).
Các đường thắng song song với nhau sẽ có cùng VTCP và có cùng VTPT nên các đường thẳng song song với trục Ox có VTPT là (0; 1) .
Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Oy?
A. (0; -3)
B. (1; -1)
C. (-3; 0)
D.( 3; 3)
Đáp án C
Trục Oy có phương trình đường thẳng là x = 0. Đường thẳng này có VTPT là ( 1; 0) và có VTCP (0; 1)
Mà các đường thẳng song song với nhau có cùng VTPT và VTCP nên câc đường thẳng song song với trục Oy có VTPT là (1; 0)
Mà 2 vecto ( 1; 0) và ( -3; 0) là 2 vecto cùng phương nên vecto ( -3; 0) cũng là VTPT của trục Oy.
Trong không gian Oxyz, cho các điểm A(6;0;0), B(0;3;0) và mặt phẳng (P): x-2y+2z=0. Gọi d là đường thẳng đi qua M(2;2;0), song song với (P) và tổng khoảng cách từ A, B đến đường thẳng d đạt giá trị nhỏ nhất. Vectơ nào dưới đây là một vectơ chỉ phương của d?
![]()
![]()
![]()
![]()
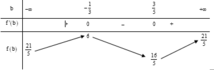
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;1;1) và mặt phẳng P : x + 2 y = 0 . Gọi Δ là đường thẳng đi qua A, song song với (P) và cách điểm B(-1;0;2) một khoảng ngắn nhất. Hỏi nhận vectơ nào dưới đây là vectơ chỉ phương.
A. u → = 6 ; 3 ; − 5
B. u → = 6 ; − 3 ; 5
C. u → = 6 ; 3 ; 5
D. u → = 6 ; − 3 ; − 5

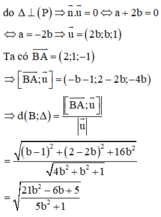

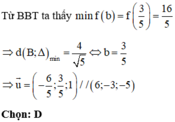
Chú ý khi giải: Các em có thể tham khảo cách 2:
+) Lập phương trình mặt phẳng (Q) đi qua A và song song với (P).
+) Khi đó Δ cần tìm là một đường thẳng nằm trong (Q) và đi qua A.

Trong không gian Oxyz, cho đường thẳng d song song với trục Oy. Đường thẳng d có một vectơ chỉ phương là
![]()
![]()
![]()
![]()
Vector nào dưới đây là 1 vector chỉ phương của đường thẳng song song với trục Ox:
A. u ⇀ = 1 ; 0
B. u ⇀ = 1 ; - 1
C. u ⇀ = 1 ; 1
D. u ⇀ = 0 ; 1
Chọn A.
Vector i ⇀ = 1 ; 0 là một vector chỉ phương trục Ox
Các đường thẳng song song với trục Ox có 1 vector chỉ phương là u ⇀ = i ⇀ = 1 ; 0
Đường thẳng d có một vectơ chỉ phương là u → = ( 3 ; - 4 ) . Đường thẳng ∆ song song với d có một vectơ pháp tuyến là:
![]()
![]()
![]()
![]()
Đáp án A
Đường thẳng ( d) có VTCP là u → = ( 3 ; - 4 )
Nên đường thẳng (d) có 1 VTPT là ( 4; 3) .
Do 2 đườg thẳng ∆ và (d) song song với nhau nên chúng có cùng VTPT và cùng VTCP .
Suy ra đường thẳng ∆ có 1 VTPT là (4; 3) .