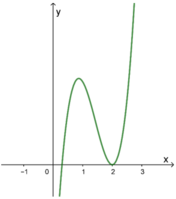
Cho hàm số bậc ba f ( x ) = a x 3 + b x 2 + c x + d có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số g ( x ) = ( x 2 - 3 x + 2 ) 2 x + 1 ( x 4 - 5 x 2 + 4 ) . f ( x ) có bao nhiêu đường tiệm cận đứng?
A. 4
B. 3
C. 2
D. 6
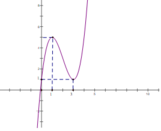
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình f(x)=3
A. 0
B. 2
C. 1
D. 3
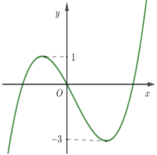
Cho hàm số bậc ba y = f ( x ) có đồ thị như hình vẽ bên. Tìm tham số m để hàm số y = f ( x ) + m có ba điểm cực trị?
![]()
![]()
![]()
![]()
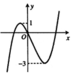
Cho hàm số bậc ba y = f(x) có đồ thị như hình bên. Tất cả các giá trị của tham số m để hàm số y = |f(x)+m| có 3 điểm cực trị là:
A. m ≤ -1 hoặc m ≥ 3
B. m ≤ -3 hoặc m ≥ 1
C. m = -1 hoặc m = 3
D. 1 ≤ m ≤ 3
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f ( x ) + m có 3 điểm cực trị?
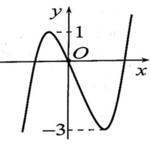
A. 1 ≤ m ≤ 3
B. m = -1 hoặc m = 3
C. m ≤ -1 hoặc m ≥ 3
D. m ≤ -3 hoặc m ≥ 1
cho hàm số y=f(x)=4x+a-√3 (2x+1)
a, chứng tỏ rằng hàm số là hàm số bậc nhất đồng biến
b, tìm x để f(x)=0
a: \(f\left(x\right)=4x+a-\sqrt{3}\left(2x+1\right)\)
\(=4x+a-2\sqrt{3}\cdot x-\sqrt{3}\)
\(=x\left(4-2\sqrt{3}\right)-\sqrt{3}+a\)
Vì \(4-2\sqrt{3}=\left(\sqrt{3}-1\right)^2>0\)
nên hàm số \(y=f\left(x\right)=x\left(4-2\sqrt{3}\right)+a-\sqrt{3}\) luôn đồng biến trên R
b: f(x)=0
=>\(x\left(4-2\sqrt{3}\right)+a-\sqrt{3}=0\)
=>\(x\left(4-2\sqrt{3}\right)=-a+\sqrt{3}\)
=>\(x=\dfrac{-a+\sqrt{3}}{4-2\sqrt{3}}\)
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f ( x - 1 ) - m - 1 có 3 điểm cực trị?
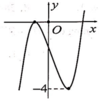
A. -1<m<5
B. - 1 ≤ m ≤ 5
C. m ≥ - 1 hoặc m ≤ - 5
D. m>-1 hoặc m<-5
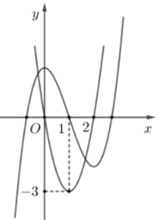
Cho hàm số bậc ba f(x) = x 3 + b x 2 + c x + d . Biết đồ thị của hàm số y = f'(x) như hình vẽ. Giá trị của c b là
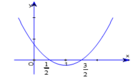
A. - 1 3
B. 3 4
C. 1 3
D. - 3 4
Chọn D
Tập xác định D = ℝ
Đạo hàm cấp 1 ![]()
Dựa vào đồ thị của hàm số y = f'(x) ta có bảng thiên của hàm số f(x)
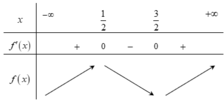
Ta có ![]()
![]()
Dựa vào bảng biến thiên ta có 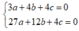
![]()
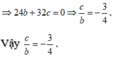
Cho hàm số đa thức bậc ba y=f(x) có đồ thị của các hàm số y=f(x), y=f '(x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)=3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng
A. 0
B. -6
C. -7
D. -5
Ta có ![]()
![]()
Quan sát đồ thị có 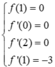
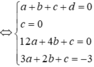

![]()
Đặt ![]() phương trình trở thành:
phương trình trở thành:
![]()
![]()
![]()
Khi đó ![]()
Phương trình này có 3 nghiệm phân biệt
![]()
Tổng các phần tử củaS bằng 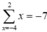
Chọn đáp án C.
Cho hàm số đa thức bậc ba y=f(x) có đồ thị như hình bên. Tìm tất cả các giá trị của tham số m để hàm số y = | f ( x ) + m | có ba điểm cực trị
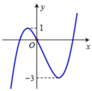
A. m ≤ - 1 hoặc m ≥ 3
B. m ≤ - 2 hoặc m ≥ 3
C. m ≤ - 1 hoặc m ≥ 5
D. 1 ≤ m ≤ 3
Cho hàm số bậc 3:y=f(x) có đồ thị như hình vẽ.
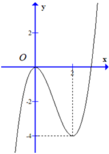
Xét hàm số g(x)=f[(x)]. Trong các mệnh đề dưới đây:
g(x) đồng biến trên (-∞;0) và (2;+∞).
Hàm số g(x) có bốn điểm cực trị.
m a x - 1 ; 1 g x = 0 .
Phương trình g(x)=0 có ba nghiệm.
Số mệnh đề đúng là
A. 3.
B. 2.
C. 1.
D. 4.