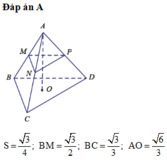
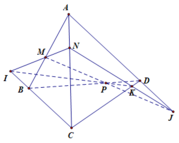
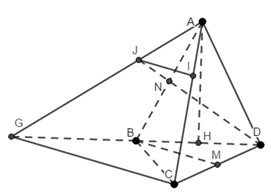
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho A M A B = A N A C ; gọi I và J lần lượt là trung điểm của BD, CD. Tứ giác MNJI là hình gì. Tìm điều kiện để tứ giác MNJI là hình bình hành.

Những câu hỏi liên quan
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho A M A B = A N A C ; gọi I và J lần lượt là trung điểm của BD, CD. Chứng minh rằng: BC // (MNI)
Ta có:
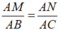
suy ra MN // BC (1) (Định lý Ta-lét đảo).
- Lại có: MN ∩ (MNI) (2)
- Từ (1) và (2) suy ra: BC // (MNI)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi K là điểm thuộc cạnh CD sao cho 2KD3KC và I là điểm thuộc đoạn thẳng BK sao cho IK2IB. Mặt phẳng left(alpharight) đi qua I và luôn cắt các tia AB, AC, AD lần lượt tại các điểm M, N, P (khác đỉnh A). Tìm giá trị nhỏ nhất của biểu thức:
T4.dfrac{AB^2}{AM^2}+9.dfrac{AC^2}{AN^2}+16.dfrac{AD^2}{AP^2}
Đọc tiếp
Cho tứ diện ABCD. Gọi K là điểm thuộc cạnh CD sao cho \(2KD=3KC\) và I là điểm thuộc đoạn thẳng BK sao cho \(IK=2IB\). Mặt phẳng \(\left(\alpha\right)\) đi qua I và luôn cắt các tia AB, AC, AD lần lượt tại các điểm M, N, P (khác đỉnh A). Tìm giá trị nhỏ nhất của biểu thức:
\(T=4.\dfrac{AB^2}{AM^2}+9.\dfrac{AC^2}{AN^2}+16.\dfrac{AD^2}{AP^2}\)
Cho tứ diện đều ABCD có cạnh bằng a, trên các cạnh AB, AC, AD lần lượt lấy các điểm M, N, P sao cho AB 2 AM, AN 2NC, AD 2 AP. Thể tích của khối tứ diện AMNP là: A.
a
3
2
72
B.
a
3
3
48
C. ...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a, trên các cạnh AB, AC, AD lần lượt lấy các điểm M, N, P sao cho AB = 2 AM, AN= 2NC, AD = 2 AP. Thể tích của khối tứ diện AMNP là:
A. a 3 2 72
B. a 3 3 48
C. a 3 2 48
D. a 3 2 12
Cho tứ diện ABCD. Các điểm M, N, P lần lượt thuộc các cạnh AB, AD, BC sao cho:
\(\frac{{AM}}{{AB}} = \frac{1}{3},\frac{{AN}}{{AD}} = \frac{2}{3},\frac{{BP}}{{BC}} = \frac{3}{4}\)
a) Xác định E. F lần lượt là giao điểm của các đường thẳng AC, BD với mặt phẳng (MNP)
b) Chứng minh rằng các đường thẳng NE, PE và CD cùng đi qua một điểm
Tham khảo:
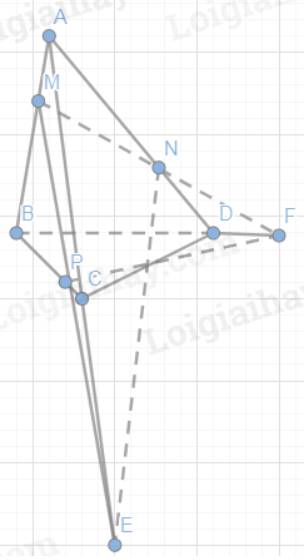
a) Tam giác ABC có: MP cắt AC tại E
Mà MP thuộc (MNP)
Nên E là giao điểm của AC và (MNP)
Tam giác ABD có: MN cắt BD tại F
Mà MN thuộc (MNP)
Nên F là giao điểm của BD và (MNP)
b) Ta có: P thuộc BC
F thuộc BD
Suy ra PF thuộc (BCD)
Do đó PF và CD cùng thuộc (BCD)
Nên PF và CD cắt nhau tại một điểm (1)
Ta có: N thuộc AD
E thuộc AC
Suy ra NE thuộc (ACD)
Do đó NE và CD cắt nhau tại một điểm (2)
Từ (1) và (2) suy ra: NE, PE, CD cùng đi qua một điểm
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là: A. Tam giác MNE B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD
C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC
D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Đáp án C
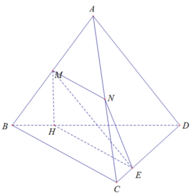
Xét (MNE) và (BCD) có:
E là điểm chung
BC // MN ⇒ BC // (MNE)
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua E và song song BC
d cắt BD tại H
⇒ MNEH là thiết diện cần tìm
Xét tứ giác MNEH có MN // EH ( // BC)
⇒ MNEH là hình thang
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi M; N; P lần lượt là các điểm thuộc cạnh AB; AC; BD;
M
N
∩
B
C
I
;
M
P
∩
A
D
J
;
N
J
∩
I
P
K
. Tìm mệnh đề đúng: A. C; D; I thẳng hàng B. C; M; K thẳng hàng C. C; D; K thẳng hàng D. M; I; J thẳng hàng
Đọc tiếp
Cho tứ diện ABCD. Gọi M; N; P lần lượt là các điểm thuộc cạnh AB; AC; BD; M N ∩ B C = I ; M P ∩ A D = J ; N J ∩ I P = K . Tìm mệnh đề đúng:
A. C; D; I thẳng hàng
B. C; M; K thẳng hàng
C. C; D; K thẳng hàng
D. M; I; J thẳng hàng
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy
I
∈
A
C
,
J
∈
D
N
sao cho IJ // BM. Độ dài IJ theo a là A.
a
3
3
B.
a
2
3
C.
a...
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy I ∈ A C , J ∈ D N sao cho IJ // BM. Độ dài IJ theo a là
A. a 3 3
B. a 2 3
C. a 3 4
D. a 2 2
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy
I
∈
A
C
,
J
∈
D
N
sao cho IJ // BM. Độ dài IJ theo a là: A.
a
3
3
B....
Đọc tiếp
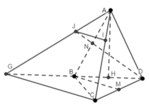
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy I ∈ A C , J ∈ D N sao cho IJ // BM. Độ dài IJ theo a là:
A. a 3 3
B. a 2 3
C. a 3 4
D. a 2 2
Đáp án A
Kẻ đường thẳng qua C song song với BM cắt BD ở G, AG cắt DN ở J, đường thẳng qua J song song với CG cắt AC ở I.
Kẻ AH vuông góc với BD tại H.
Dễ dàng chứng minh được IJ//BM; B là trung điểm của GD và tính được
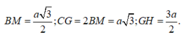
Ta có: Tam giác ANJ đồng dạng với tam giác AHG nên:

Mà IJ//CG nên:
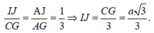
Đúng 0
Bình luận (0)
Cho tứ diện \(ABCD\) và điểm \(M\) thuộc cạnh \(AB\). Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(BC\) và \(AD\). Gọi \(N,P,Q\) lần lượt là giao điểm của mặt phẳng \(\left( \alpha \right)\) với các cạnh \(AC,CD\) và \(DB\).
a) Chứng minh \(MNPQ\) là hình bình hành.
b) Trong trường hợp nào thì \(MNPQ\) là hình thoi?
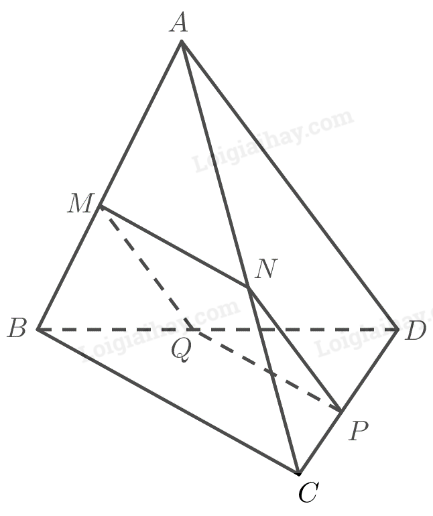
a) Ta có:
\(\begin{array}{l}MN = \left( \alpha \right) \cap \left( {ABC} \right)\\PQ = \left( \alpha \right) \cap \left( {BC{\rm{D}}} \right)\\BC = \left( {ABC} \right) \cap \left( {BC{\rm{D}}} \right)\\MN\parallel BC\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel PQ\parallel BC\) (1).
\(\begin{array}{l}MQ = \left( \alpha \right) \cap \left( {ABD} \right)\\NP = \left( \alpha \right) \cap \left( {AC{\rm{D}}} \right)\\A{\rm{D}} = \left( {ABD} \right) \cap \left( {AC{\rm{D}}} \right)\\MQ\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MQ\parallel NP\parallel A{\rm{D}}\) (2).
Từ (1) và (2) suy ra \(MNPQ\) là hình bình hành.
b) Để \(MNPQ\) là hình thoi thì \(MN = NP\).
Ta có:
\(\begin{array}{l}MN\parallel BC \Rightarrow \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}\\NP\parallel A{\rm{D}} \Rightarrow \frac{{NP}}{{A{\rm{D}}}} = \frac{{CN}}{{AC}} \Rightarrow \frac{{MN}}{{A{\rm{D}}}} = \frac{{CN}}{{AC}}\end{array}\)
Ta có:
\(\begin{array}{l}\frac{{AN}}{{AC}} + \frac{{CN}}{{AC}} = 1 \Leftrightarrow \frac{{MN}}{{BC}} + \frac{{MN}}{{A{\rm{D}}}} = 1 \Leftrightarrow MN.\left( {\frac{1}{{BC}} + \frac{1}{{A{\rm{D}}}}} \right) = 1\\ \Leftrightarrow MN.\frac{{BC + A{\rm{D}}}}{{BC.A{\rm{D}}}} = 1 \Leftrightarrow MN = \frac{{BC.A{\rm{D}}}}{{BC + A{\rm{D}}}}\end{array}\)
Vậy nếu \(MN = \frac{{BC.A{\rm{D}}}}{{BC + A{\rm{D}}}}\) thì \(MNPQ\) là hình thoi.
Đúng 0
Bình luận (0)