Cho cấp số cộng ( u n ) có u 4 = - 12 ; u 14 = 18 . Tìm u 1 , d của cấp số cộng?
A. u 1 = - 21 , d = 3 .
B. u 1 = - 21 , d = - 3 .
C. u 1 = 20 , d = - 3 .
D. u 1 = - 22 , d = 3 .
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Cho cấp số cộng (un) có u4=-12, u14=18. Tính tổng 16 số hạng đầu tiên cua cấp số cộng này
\(\left\{{}\begin{matrix}u_{14}=u_1+13d=18\\u_4=u_1+3d=-12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}d=3\\u_1=-21\end{matrix}\right.\)
Tổng 16 số hạng đầu tiên:
\(S_{16}=\frac{16\left(2u_1+15d\right)}{2}=24\)
cho (Un) là cấp số cộng U3 +U13=80 .tổng 15 số hạng đầu tiên của cấp số cộng đố bằng bao nhiêu
Cho cấp số cộng có tổng n số hạng đầu là S n = 3 n 2 + 4 n , n ∈ ℕ * . Giá trị của số hạng thứ 10 của cấp số cộng là
A. u 10 = 55
B. u 10 = 67
C. u 10 = 61
D. u 10 = 59
Đáp án C
Gọi số hạng đầu và công sai u 1 , d ta có S n = n 2 2 u 1 + n - 1 d = 3 n 2 + 4 n
⇒ 2 u 1 - d + n d = 8 + 6 n ⇒ 2 u 1 - d = 8 d = 6 ⇒ u 1 = 7 d = 6 ⇒ u 10 = 61 .
Cho cấp số cộng có tổng n số hạng đầu là S n = 3 n 2 + 4 n , n ∈ ℕ * . Giá trị của số hạng thứ 10 của cấp số cộng là
A. u 10 = 67 .
B. u 10 = 61 .
C. u 10 = 59 .
D. u 10 = 55 .
Chọn B
Ta có: S n = 3 n 2 + 4 n = n ( 7 + 6 n + 1 ) 2
⇒ u n = 6 n + 1 ⇒ u 10 = 61
Cho cấp số cộng có tổng n số hạng đầu là S n = 3 n 2 + 4 n , n ∈ ℕ * . Giá trị của số hạng thứ 10 của cấp số cộng là
A. u 10 = 67
B. u 10 = 61 .
C. u 10 = 59 .
D. u 10 = 55
Cho cấp số cộng (un) có công thức tổng quát là un =5-2n, n ∈ N * Tính tổng 20 số hạng đầu tiên của cấp số cộng.
A. -350
B. 440
C. -320
D. -340
Cho cấp số cộng có tổng n số hạng đầu là S n = 3 n 2 + 4 n với n ∈ ℕ + . Giá trị của số hạng thứ 10 của cấp số cộng là
A. u 10 = 55.
B. u 10 = 67.
C. u 10 = 59.
D. u 10 = 61.
Cho cấp số cộng (un) có số hạng đầu là u1 = 1 và công sai d = 1. Tìm n sao cho tổng của n số hạng đầu tiên của cấp số cộng đó bằng 3003.
A. n = 79
B. n = 78
C. n = 77
D. n = 80
Chọn C
- Do công sai và số hạng đầu là d = 1, u 1 = 1 nên đây là tổng của n số tự nhiên đầu tiên là:
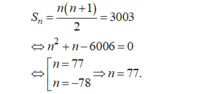
1. Cho 3 số lập thành cấp số cộng. Biết tổng 3 số bằng 6 và tổng bình phương 3 số bằng 30. Tìm các số.
2. Tìm m để phương trình sau có 4 nghiệm lập thành cấp số cộng:
\(x^4-10x^2+9m=0\)
3. Cho cấp số cộng giảm thỏa mãn:
\(\left\{{}\begin{matrix}u_1+u_2+u_3=3\\u_3^2-u_2^2=3\end{matrix}\right.\)
Tính: \(S=\dfrac{1}{u_1u_2}+\dfrac{1}{u_2u_3}+...+\dfrac{1}{u_{19}u_{20}}\)
4. Cho cấp số cộng tăng:
\(\left\{{}\begin{matrix}u_1+u_3+u_5=-3\\u_2+u_4+u_6=3\end{matrix}\right.\)
Tính: \(S=u_1+u_4+u_7+...+u_{88}\)
Mọi người giúp mình với ạ!!! Mình cảm ơn mọi người nhiều!!!
Câu 1: Gọi 3 số là a;b;c
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=6\\2b=a+c\\a^2+b^2+c^2=30\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\a+c=4\\a^2+c^2=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}b=2\\c=4-a\\a^2+\left(4-a\right)^2=26\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\c=5\\a=-1\end{matrix}\right.\left(\text{V\text{ì} }a< c\right)\)
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)