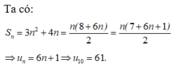Các câu hỏi tương tự
Cho cấp số cộng có tổng n số hạng đầu là
S
n
3
n
2
+
4
n
,
n
∈
ℕ
*
. Giá trị của số hạng thứ 10 của cấp số cộng là A.
u
10
55
B.
u
10
67
C.
u
10
61
D. ...
Đọc tiếp
Cho cấp số cộng có tổng n số hạng đầu là S n = 3 n 2 + 4 n , n ∈ ℕ * . Giá trị của số hạng thứ 10 của cấp số cộng là
A. u 10 = 55
B. u 10 = 67
C. u 10 = 61
D. u 10 = 59
Cho cấp số cộng có tổng n số hạng đầu là
S
n
3
n
2
+
4
n
với
n
∈
ℕ
+
. Giá trị của số hạng thứ 10 của cấp số cộng là A.
u
10
55.
B.
u
10
67.
C.
u
10...
Đọc tiếp
Cho cấp số cộng có tổng n số hạng đầu là S n = 3 n 2 + 4 n với n ∈ ℕ + . Giá trị của số hạng thứ 10 của cấp số cộng là
A. u 10 = 55.
B. u 10 = 67.
C. u 10 = 59.
D. u 10 = 61.
Cho dãy số u n , n ∈ ℕ * là cấp số cộng có u 4 + u 7 = 5 . Tính tổng 10 số hạng đầu tiên của dãy số đó.
A. 25
B. 50
C. 3
D. 60
Cho cấp số cộng
u
n
với số hạng đầu
u
1
2
và số hạng thứ năm
u
5
14
. Tổng của 10 số hạng đầu của cấp số cộng
u
n
là A. 232 B. 126 C. 155 D. 187
Đọc tiếp
Cho cấp số cộng u n với số hạng đầu u 1 = 2 và số hạng thứ năm u 5 = 14 . Tổng của 10 số hạng đầu của cấp số cộng u n là
A. 232
B. 126
C. 155
D. 187
Một cấp số cộng có tổng của n số hạng đầu
S
n
tính theo công thức
S
n
5
n
2
+
3
n
,
n
∈
ℕ
*
.
Tìm số hạng đầu
u
1
và công sai d của cấp số cộng đó. A....
Đọc tiếp
Một cấp số cộng có tổng của n số hạng đầu S n tính theo công thức S n = 5 n 2 + 3 n , n ∈ ℕ * . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó.
A. u 1 = − 8 ; d = 10
B. u 1 = − 8 ; d = − 10
C. u 1 = 8 ; d = 10
D. u 1 = 8 ; d = − 10
Một cấp số cộng có tổng của n số hạng đầu
S
n
tính theo công thức
S
n
5
n
2
+
3
n
n
∈
ℕ
*
. Tìm số hạng đầu
u
1
và công sai d của cấp số cộng đó A.
u
1...
Đọc tiếp
Một cấp số cộng có tổng của n số hạng đầu S n tính theo công thức S n = 5 n 2 + 3 n n ∈ ℕ * . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó
A. u 1 = - 8 ; d = 10
B. u 1 = - 8 ; d = - 10
C. u 1 = 8 ; d = 10
D. u 1 = 8 ; d = - 10
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C. 20
D. 17
Cho cấp số cộng có tổng 10 số hạng đầu tiên và 100 số hạng đầu tiên lần lượt là 100 và 10. Khi đó tổng của 110 số hạng đầu tiên là:
A. 90
B. - 90
C. - 110
D. - 23
Cho
u
n
là một cấp số cộng có tổng n số hạng đầu tính được theo công thức
S
n
5
n
2
+
3
n
với
n
∈
N
*
. Số hạng đầu
u
1
và công sai d của cấp số cộng đó là A.
u...
Đọc tiếp
Cho u n là một cấp số cộng có tổng n số hạng đầu tính được theo công thức S n = 5 n 2 + 3 n với n ∈ N * . Số hạng đầu u 1 và công sai d của cấp số cộng đó là
A. u 1 = - 8 d = 10
B. u 1 = - 8 d = - 10
C. u 1 = 8 d = 10
D. u 1 = 8 d = - 10