Cho n là số nguyên dương thỏa mãn C n 2 - C n 1 = 44 Số hạng không chứa x trong khai triển của biểu thức ( x x + 1 x 4 ) n , với x > 0 bằng:
A.165.
B.485.
C.238.
D.525.
Cho n là số nguyên dương thỏa mãn C n 2 - C n 1 = 44 . Số hạng không chứa x trong khai triển của biểu thức x x + 1 x 4 n , với x > 0 bằng
A. 165
B. 485
C. 238
D. 525
cho n là số nguyên dương thỏa mãn c1n + c 2 n = 15 tìm số hạng không chứa x trong khai triển (x+2/x^4) A. 10 B.20 C.6 D.1
Giúp vs b
\(C^1_n+C^2_n=15\)
=>\(n+\dfrac{n!}{\left(n-2\right)!\cdot2!}=15\)
=>\(n+\dfrac{n^2-n}{2}=15\)
=>2n+n^2-n=30
=>n^2+n-30=0
=>n=5
=>(x+2/x^4)^5
SHTQ là: \(C^k_5\cdot x^{5-k}\cdot\left(\dfrac{2}{x^4}\right)^k=C^k_5\cdot x^{5-5k}\cdot2^k\)
SỐ hạng ko chứa x tương ứng với 5-5k=0
=>k=1
=>Số hạng đó là 5*2=10
Cho n là số nguyên dương thỏa mãn C n 2 - C n 1 = 44 . Hệ số của số hạng chứa trong khai triển biểu thức x 4 - 2 x 3 n bằng:
A. 29568.
B. - 1774080
C. - 14784
D. 14784.
Cho n là số nguyên dương thỏa mãn C n 2 - C n 1 = 44 . Hệ số của số hạng chứa x 9 trong khai triển biểu thức x 4 - 2 x 3 n bằng
A. 14784
B. 29568
C. -1774080
D. -14784
Chọn D
Điều kiện xác định: ![]() .
.
Khi đó
![]()
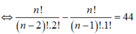
![]()
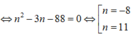
Kết hợp với điều kiện xác định suy ra n = 11
Ta có: 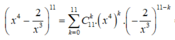
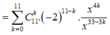
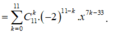 .
.
Số hạng chứa x 9 ứng với k thỏa 7k - 33 = 9 => k = 6
Vậy hệ số của số hạng chứa
x
9
là ![]() .
.
Với số nguyên dương n thỏa mãn C n 2 − n = 27 , trong khai triển x + 2 x 2 n số hạng không chứa x là:
A. 84
B. 8
C. 5376
D. 672
Đáp án D.
Phương pháp
Sử dụng công thức C n k = n ! k ! n − k ! tìm n.
Sử dụng khai triển nhị thức Newton
a + b n = ∑ k = 0 n C n k . a n − k . b k
Cách giải
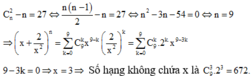
Cho n là số nguyên dương thỏa mãn C n 1 + C n 2 = 78. Số hạng không chứa x trong khai triển x + 2 x 3 n bằng
A. 3960
B. 220
C. 1760
D. 59136
Chọn C
Điều kiện: ![]()

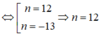 ( do điều kiện (1))
( do điều kiện (1))
Khi đó, 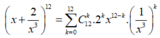
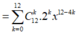
Số hạng không chứa x tương ứng 12 - 4k = 0 => k = 3
Suy ra số hạng không chứa x là: ![]()
Với các số nguyên dương n thỏa mãn C n 2 - n = 27 , trong khai triển x + 2 x 2 n số hạng không chứa x là:
A. 84
B. 8
C. 5376
D. 672
a) CHO 3 SỐ DƯƠNG a , b , c THỎA MÃN abc=1 . CMR: (a+b)(b+c)(c+a)>= 2(1+a+b+c)
b) CHO m,n LÀ 2 SỐ NGUYÊN DƯƠNG THỎA MÃN: m^2+n^2+2018 CHIA HẾT CHO mn. CMR m,n LÀ 2 SỐ LẺ VÀ NGUYÊN TỐ CÙNG NHAU
m.n/(m^2+n^2 ) và m.n/2018
- Đặt (m,n)=d => m= da;n=db ; (a,b)=1
=> d^2(a^2+b^2)/(d^2(ab)) = (a^2+b^2)/(ab) => b/a ; a/b => a=b=> m=n=> ( 2n^2+2018)/n^2 =2 + 2018/n^2 => n^2/2018
=> m=n=1 ; lẻ và nguyên tố cùng nhau. vì d=1
Vẽ SH _I_ (ABCD) => H là trung điểm AD => CD _I_ (SAD)
Vẽ HK _I_ SD ( K thuộc SD) => CD _I_ HK => HK _I_ (SCD)
Vẽ AE _I_ SD ( E thuộc SD).
Ta có S(ABCD) = 2a² => SH = 3V(S.ABCD)/S(ABCD) = 3(4a³/3)/(2a²) = 2a
1/HK² = 1/SH² + 1/DH² = 1/4a² + 1/(a²/2) = 9/4a² => HK = 2a/3
Do AB//CD => AB//(SCD) => khoảng cách từ B đến (SCD) = khoảng cách từ A đến (SCD) = AE = 2HK = 4a/3
Biết n là số nguyên dương thỏa mãn C n n - 1 + C n n - 2 = 78 , số hạng chứa x 8 trong khai triển ( x 3 - 2 x ) n là
A.-10176 x 8
B.-101376
C.-112640
D.101376 x 8