Tìm nguyên hàm F(x) của hàm số f(x)=sinx+cosx thỏa mãn F π 2 = 2
A. F (x)= -cosx +sinx+1
B. F (x)= -cosx+sinx-1
C. F(x)= cosx-sinx +3
D. F (x)= -cosx+sinx +3
cho hàm số f(x) = \(\dfrac{\left(sinx+2x\right)\left[\left(x^2+1\right)sinx-x\left(cosx+2\right)\right]}{\left(cosx+2\right)^2\sqrt{\left(X^2+1\right)^3}}\). Biết F(x) là một nguyên hàm của f(x) và F(0)=2021. Tính giá trị biểu thức T=F(-1) + F(1).
cho hàm số \(f\left(x\right)=\dfrac{\left(sinx+2x\right)\left[\left(x^2+1\right)sinx-x\left(cosx+2\right)\right]}{\left(cosx+2\right)^2\sqrt{\left(x^2+1\right)^3}}\). Biết F(x) là một nguyên hàm của f(x) và F(0)=2021. Tính giá trị biểu thức T=F(-1) + F(1).
Tìm nguyên hàm của hàm số f ( x ) = ( sin x + cos x ) 2
![]()
![]()
![]()
![]()
Tìm nguyên hàm F(x) của f(x) = cosx + sinx biết F(0) = 1.
A. F(x) = sinx – cosx + 2
B. F(x) = –sinx + cosx – 1
C. F(x) = sinx – cosx + 1
D. F(x) = –sinx + cosx
Tìm nguyên hàm F(x) của f(x)=cosx +sinx, biết F(0)=1.
A. F(x) = sinx –cosx +2
B. F(x) = -sinx +cosx -1
C. F(x) = sinx –cosx +1
D. F(x) = -sinx +cosx
Cho hàm f : [ 0 ; π 2 ] → R là hàm liên tục thỏa mãn ∫ 0 π 2 [ f ( x ) ] 2 - 2 f ( x ) ( sin x - cos x ) ] d x = 1 - π 2 . Tính ∫ 0 π 2 f ( x ) d x .
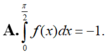
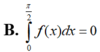
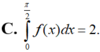
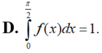
Nguyên hàm của hàm số f ( x ) = sin x . 2 - cos x là
![]()
![]()
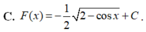

Nguyên hàm của hàm số f ( x ) = cos x ( 2 + sin x ) 2 là:
A. ∫ f ( x ) d x = sin x ( 2 + sin x ) 2 + C
B. ∫ f ( x ) d x = 1 2 + sin x + C
C. ∫ f ( x ) d x = - 1 2 + sin x + C
D. ∫ f ( x ) d x = sin x 2 + sin x + C
Tìm x > 0 thỏa mãn hàm số f(x) = 0.6*sinx+0.8*cosx là bé nhất