Gọi (C) là đồ thị của hàm số y = lo 2018 x và C ' là đồ thị của hàm số y = f(x) , C ' đối xứng với (C) qua trục tung. Hàm số y = f x đồng biến trên khoảng nào sau đây?
![]()
![]()
![]()
![]()
Gọi (C) là đồ thị của hàm số y = log 2018 x và (C’) là đồ thị của hàm số y = f x , (C’) đối xứng với (C) qua trục tung. Hàm số y = f x đồng biến trên khoảng nào sau đây?
![]()
![]()
![]()
![]()
Biết đồ thị (C) ở hình bên là đồ thị hàm số y = a x a > 0 , a ≠ 1 . Gọi (C’) là đường đối xứng với (C) qua đường thẳng y=x
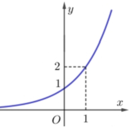
Hỏi (C’) là đồ thị của hàm số nào dưới đây?
A. y = log 1 2 x .
B. y = 2 x .
C. y = 1 2 x .
D. y = log 2 x .
Hàm số y = f(x) có đạo hàm trên R \ { -2; 2}, có bảng biến thiên như sau:
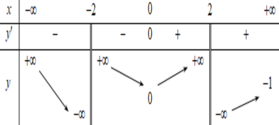
Gọi k, l lần lượt là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 f ( x ) - 2018 . Tính k + l
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đáp án C
Vì phương trình ![]() có ba nghiệm phân biệt nên đồ thị hàm số
có ba nghiệm phân biệt nên đồ thị hàm số 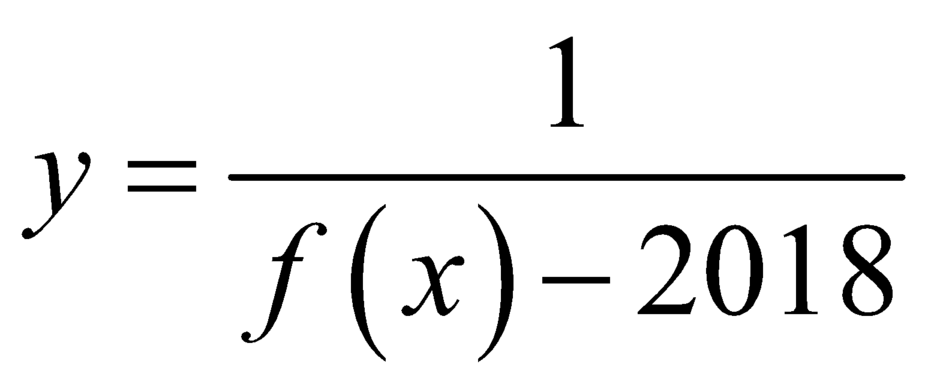 có ba đường tiệm cận đứng.
có ba đường tiệm cận đứng.
Mặt khác, ta có:
![]()
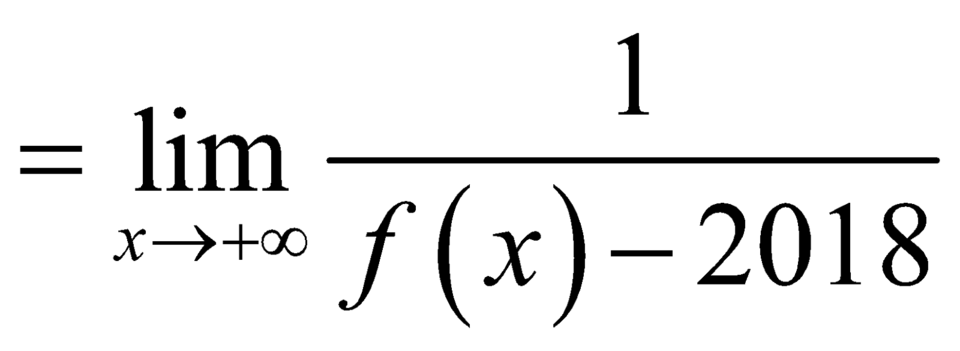
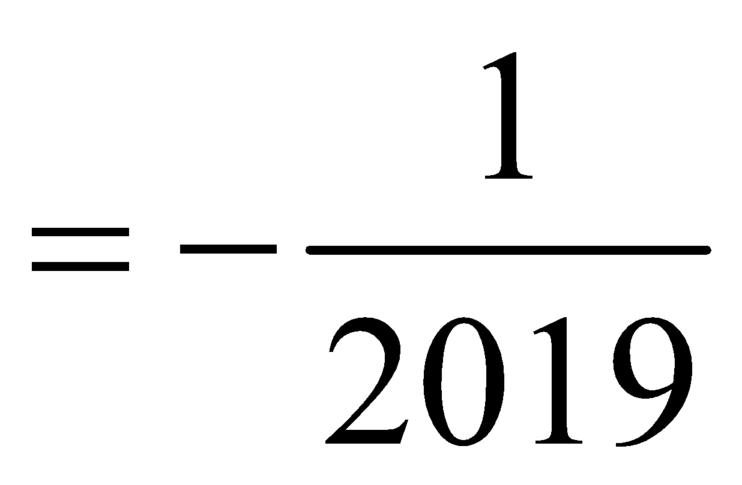 nên đường thẳng
nên đường thẳng ![]() là đường tiệm cận ngang của đồ thị hàm số
là đường tiệm cận ngang của đồ thị hàm số 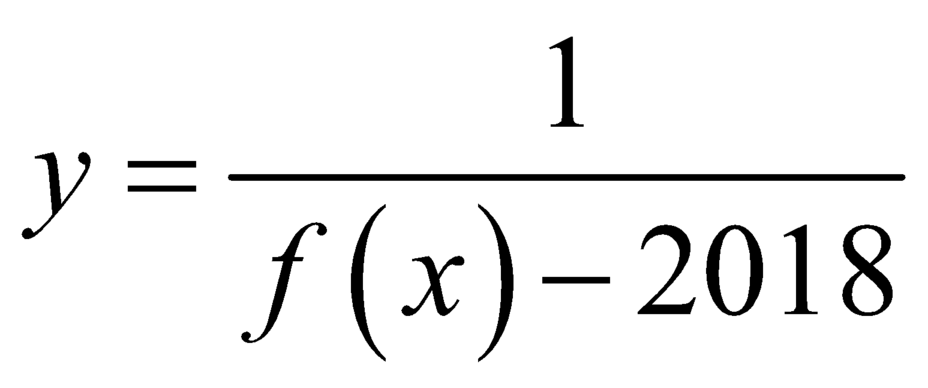 .
.
Và ![]()
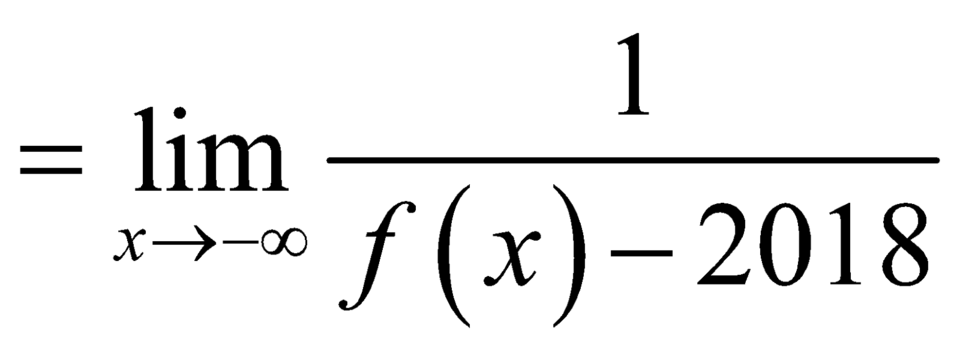
![]() nên đường thẳng y=0 là đường tiệm cận ngang của đồ thị hàm số
nên đường thẳng y=0 là đường tiệm cận ngang của đồ thị hàm số 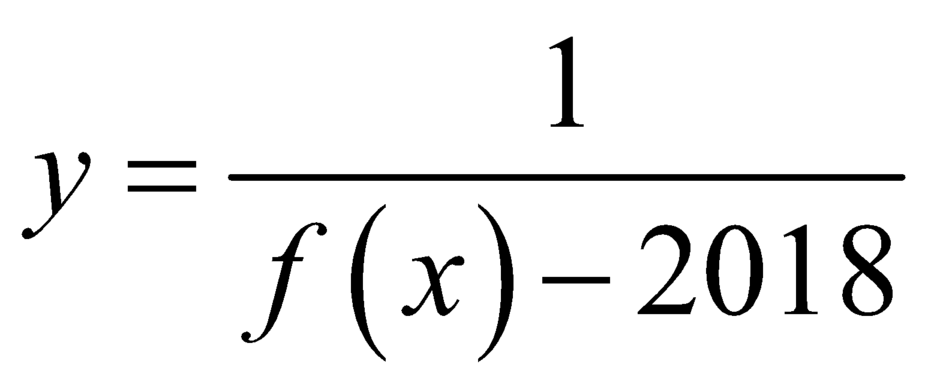 .
.
Vậy ![]() .
.
Hàm số y = f(x) có đạo hàm trên ℝ \ − 2 ; 2 , có bảng biến thiên như sau:
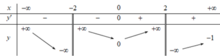
Gọi k, l lần lượt là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 f x − 2018
Tính k + l
A. k + l = 3
B. k + l = 4
C. k + l = 5
D. k + l = 2
Cho hai hàm số y=f(x) và y=g(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số y=f’(x) là đường cong nét đậm, đồ thị hàm số y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [a;c]

A. m i n h x a ; c = h 0
B. m i n h x a ; c = h a
C. m i n h x a ; c = h b
D. m i n h x a ; c = h c
Hàm số y = f(x) có đạo hàm trên R \ {-2; 2}, có bảng biến thiên như sau:
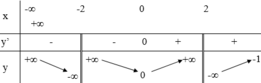
Gọi k, l lần lượt là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 f x - 2018 . Tính k+l
A. k+l =2
B. k+l =3
C. k+l =4
D. k+l =5
Cho hàm số y = f x xác định trên ℝ và có đồ thị hàm số y = f ' x như hình vẽ:
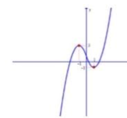
Số tiếp tuyến của đồ thị hàm số f x vuông góc với đường thẳng x + 4 y + 2018 = 0 là
A.4
B. 3
C. 2
D. 1.
Chọn D.
Tiếp tuyến vuông góc với đường thẳng x + 4 y + 2018 = 0 nên hệ số góc tiếp tuyến là k=4
Hoành độ tiếp điểm là nghiệm của phương trình f ' x = 4 . 1
Dựa vào hình vẽ ở đề bài ta thấy đường thẳng y=4 cắt đồ thị hàm số y = f ' x tại 1 điểm nên phương trình (1) có một nghiệm duy nhất. Do đó có 1 tiếp thỏa mãn đề bài.
Cho hàm số y=3x-1 có đồ thị d1 và hàm số y=-x +3 có đồ thị d2 A. Vẽ đồ thị hs trên cùng hệ trục tọa độ Oxy B. Gọi giao điểm d1, d2 với trục Õ lần lượt là A và B, giao điểm của 2 đường thẳng d1 và d2 là C. Tìm tọa độ các điểm A,B,C C. Tính số đo của góc tạo bởi đường thẳng d1 với tia Ox
a: 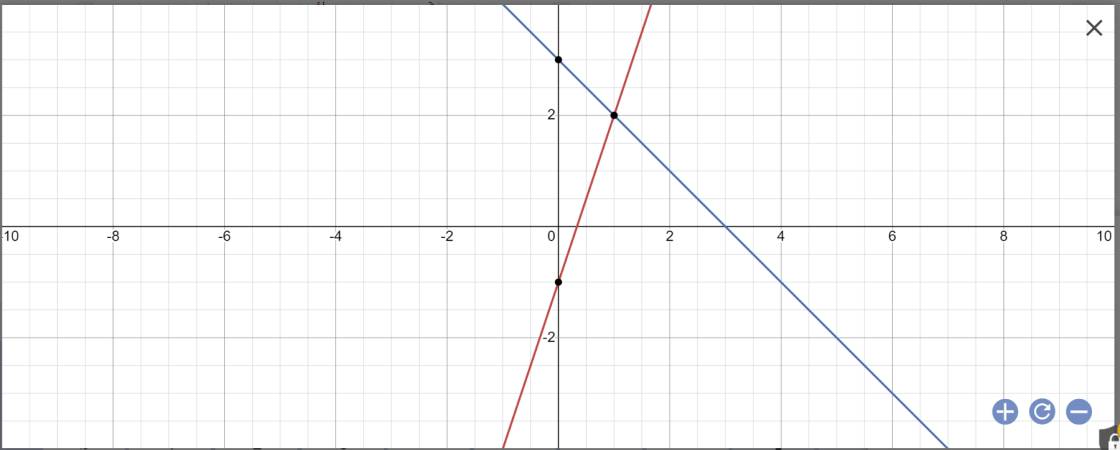
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)
Cho hàm số y = x 3 − 2 x 2 + 2 x có đồ thị (C). Gọi x 1 , x 2 là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến với (C) vuông góc với đường thẳng y = − x + 2018 . Khi đó x 1 + x 2 bằng:
A. 8 3 .
B. 2 3 .
C. 4 3 .
D. 5 3 .
Đáp án C
y ' = 3 x 2 − 4 x + 2
Do tại các điểm M, N tiếp tuyến với vuông góc với đường thẳng y = − x + 2018
nên
3 x 2 − 4 x + 2 . − 1 = − 1 ⇔ 3 x 2 − 4 x + 1 = 0 ⇔ x = 1 x = 1 3
Suy ra x 1 + x 2 = 1 + 1 3 = 4 3 .