Tìm nguyên hàm I = ∫ d x 2 x + x x + x .
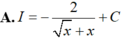
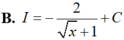
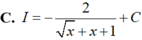
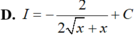
Cho biết hàm số f(x) có đạo hàm f’(x) liên tục và có một nguyên hàm là hàm số F(x). Tìm nguyên hàm I = ∫ 2 f x + f ' x + 1 d x
A. I=2F(x)+xf(x)+C
B. I=2xF(x)+x+1
C. I=2xF(x)+f(x)+x+C
D. I=2F(x)+f(x)+x+C
tìm nguyên hàm của (x+1)sin2x
tìm nguyên hàm của (x.sin(x/2)).(x.cos(x/2))
tìm nguyên hàm của 1/(x.lnx.ln(lnx))
c2 ;nhan vo duocx2(sinx/2 .cosx/2)=x2/2(sinx+cosx) lai nhan vo roi tung phan nhe
Tìm nguyên hàm \(I=\int\frac{x^2-3}{x^3-2x^2-x+2}dx\)
Ta có :\(x^3-2x^2-x+2=x\left(x^2-1\right)-2\left(x^2-1\right)=\left(x+1\right)\left(x-1\right)\left(x-2\right)\)
Ta viết biểu thức dạng \(\frac{x^2-3}{x^3-2x^2-x+2}=\frac{A_1}{x+1}+\frac{A_2}{x-1}+\frac{A_3}{x-2}\)
Từ đó
\(A_1\left(x-1\right)\left(x-2\right)+A_2\left(x+1\right)\left(x-2\right)+A_3\left(x+1\right)\left(x-1\right)\equiv x^2-3\) (1)
hay là \(\left(A_1+A_2+A_3\right)x^2+\left(-3A_1-A_2\right)x+\left(2A_1-2A_2-A_3\right)\equiv x^2-3\)
Áp dụng phương pháp cân bằng hệ số ta có
\(x^2\) \(A_1+A_2+A\)
\(x^1\) \(-3A_1-A\)
\(x^0\) \(2A_1-2A_2-A\)
\(\Rightarrow A_1=-\frac{1}{3},A_2=1,A_3=\frac{1}{3}\)
Biết F(x) là một nguyên hàm của hàm số f(x). Tìm I = ∫ 3 f x + 1 d x .
A. I = 3 F x + x + C .
B. I = 3 x F x + 1 + C .
C. I = 3 x F x + x + C .
D. I = 3 F x + 1 + C .
Đáp án A.
Ta có: ∫ 3 f x + 1 d x = 3 ∫ f x d x + x + C = 3 F x + x + C .
Cho biết F(x) là một nguyên hàm của hàm số f(x) . Tìm I = ∫ 3 f x + 2 d x
A. B.
B. I = 3 F ( x ) + 2 x + C
C. I = 3 F ( x ) + 2 + C
D. I = 3 x F ( x ) + 2 + C
Đáp án B
Phương pháp:
Sử dụng tính chất
∫ α f x ± β g ( x ) d x = α ∫ f ( x ) d x ± β ∫ g ( x ) d x
Cách giải:
Ta có:
![]()
![]()
Tìm nguyên hàm \(I=\int\frac{\left(x-1\right)dx}{x^2\left(x-2\right)\left(x+1\right)^2}\)
Khai triển biểu thức dưới dấu nguyên hàm thành tổng các phân thức đơn giản
\(\frac{\left(x-1\right)dx}{x^2\left(x-2\right)\left(x+1\right)^2}=\frac{A}{x^2}+\frac{B}{x}+\frac{C}{x-2}+\frac{D}{\left(x+1\right)^2}+\frac{E}{x-1}\)
Quy đồng mẫu số chung và cân bằng tử số của hai vế với nhau, ta có :
\(A\left(x-2\right)\left(x+1\right)^2+Bx\left(x-2\right)\left(x+1\right)^2+Cx^2\left(x+1\right)^2+Dx\left(x-2\right)+Ẽx^2\left(x+1\right)\left(x-2\right)\equiv x-1\) (a)
Để xác định các hệ số A, B, C, D, E ta thay \(x=0,x=2,x=-1\) vào (a) ta thu được \(\begin{cases}-2A=-1\\36C=1\\-3D=-2\end{cases}\) \(\Rightarrow\) \(A=\frac{1}{2},C=\frac{1}{36},D=\frac{2}{3}\)
Thay các giá trị này vào (a) và mở các dấu ngoặc ta có :
\(\left(B+E+\frac{1}{36}\right)x^4+\left(\frac{11}{9}-E\right)x^3+\left(-3B-2E-\frac{47}{36}\right)x^2+\left(-\frac{3}{2}-2B\right)x-1\equiv x-1\)
Cân bằng các hệ số của \(x^3\) và của \(x\) ta thu được :
\(\begin{cases}\frac{11}{9}-E=0\\-\frac{3}{2}-2B=1\end{cases}\) \(\Rightarrow\) \(B=-\frac{5}{4},E=\frac{11}{9}\)
Như vậy :\(A=\frac{1}{2},C=\frac{1}{36},D=\frac{2}{3}\),\(B=-\frac{5}{4},E=\frac{11}{9}\)
Từ đó suy ra :
\(I=-\frac{1}{2x}-\frac{5}{4}\ln\left|x-2\right|-\frac{2}{3\left(x+1\right)}+\frac{11}{9}\ln\left|x+1\right|+C\)
Tìm nguyên hàm của hàm số I = ∫ 2 x 2 + x + 1 x - 1
A. x 2 - 3 x + 4 ln x - 1 + C
B. x 2 + 3 x - 4 ln x - 1 + C
C. x 2 + 3 x + 4 ln x - 1 + C
D. x 2 - 3 x - 4 ln x - 1 + C
Chọn C
Ta có: 2 x 2 + x + 1 x - 1 = 2 x + 3 + 4 x - 1
Suy ra
I = ∫ 2 x + 3 + 4 x - 1 d x = x 2 + 3 x + 4 ln x - 1 + C
Tìm nguyên hàm \(I=\frac{x^2+3x-1}{x^3+4x^2+4x}dx\)
Đây là nguyên hàm của phân thức hữu tỉ thực sự. Đa thức mẫu số có hai nghiệm là \(x=0,x=-2\). Ta có \(x^3+4x^2+4x=x\left(x+2\right)^2\)
Ta viết biểu thức dạng \(\frac{x^2+3x-1}{x^3+4x^2+4x}=\frac{A}{x}+\frac{B}{x+2}+\frac{C}{\left(x+2\right)^2}\) (1)
Trong đó A, B, C là những hệ số chưa được xác định (chưa biết)
Nghiệm \(x=2\) có bội bằng 2, cho nên trong khai triển vừa viết nó tương ứng với hai số hạng.
Quy đồng rồi khử mẫu số ở hai vế (1) ta có
\(x^2+3x-1\equiv A\left(x+2\right)^2+Bx\left(x+2\right)+Cx\) (2)
Ta cần xác định các hệ số A,B,C
Cân bằng hệ số các lũy thừa cùng bậc x ở hai vế, ta có :
\(\begin{cases}A+B=1\\4A+2B+C=3\\4A=-1\end{cases}\)\(\Rightarrow\) \(A=-\frac{1}{4};B=\frac{5}{4};C=\frac{3}{2}\)
Tìm họ nguyên hàm của hàm số sau: I = ∫ x + 1 3 - 2 x 3 d x
A. 3 4 3 - 2 x 7 3 7 - 5 3 + 2 x 4 3 4 + C
B. 3 4 3 - 2 x 7 3 - 7 - 5 3 - 2 x 4 3 4 + C
C. 3 4 3 - 2 x 7 3 7 - 5 3 - 2 x 4 3 - 4 + C
D. 3 4 3 - 2 x 7 3 7 - 5 3 - 2 x 4 3 4 + C
Chọn D
Đặt t = 3 - 2 x 3 ⇒ t 3 = 3 - 2 x ⇔ x = 3 - t 3 2 ⇒ d x = - 3 2 t 2 d t
⇒ I = - 3 2 ∫ 3 - t 3 2 + 1 t . t 2 d t = - 3 4 ∫ ( 5 t 3 - t 6 ) d t = - 3 4 5 t 4 4 - t 7 7 + C = 3 4 3 - 2 x 7 3 7 - 5 3 - 2 x 4 3 4 + C
Tìm nguyên hàm I = ∫ x + 5 x d x .
A. I = x - 5 ln x + C
B. I = x - 5 x 2 + C
C. I = x + 5 ln x + C
D. I = x + 5 x 2 + C