Chọn D
Đặt t = 3 - 2 x 3 ⇒ t 3 = 3 - 2 x ⇔ x = 3 - t 3 2 ⇒ d x = - 3 2 t 2 d t
⇒ I = - 3 2 ∫ 3 - t 3 2 + 1 t . t 2 d t = - 3 4 ∫ ( 5 t 3 - t 6 ) d t = - 3 4 5 t 4 4 - t 7 7 + C = 3 4 3 - 2 x 7 3 7 - 5 3 - 2 x 4 3 4 + C
Chọn D
Đặt t = 3 - 2 x 3 ⇒ t 3 = 3 - 2 x ⇔ x = 3 - t 3 2 ⇒ d x = - 3 2 t 2 d t
⇒ I = - 3 2 ∫ 3 - t 3 2 + 1 t . t 2 d t = - 3 4 ∫ ( 5 t 3 - t 6 ) d t = - 3 4 5 t 4 4 - t 7 7 + C = 3 4 3 - 2 x 7 3 7 - 5 3 - 2 x 4 3 4 + C
Họ nguyên hàm của hàm số f ( x ) = x 2 + 2 x - 3 ( x + 1 ) 2 là
![]()
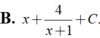
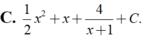
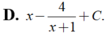
trong các hàm số sau hàm số nào đồng biến trên R: A. y= 2x-1/x+2 B. y= -x^3+x^2-5x C. y= x^3+2x+1 D.-x^4-2x^2+3
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1 là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
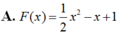
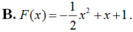
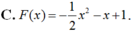
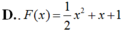
Tìm nguyên hàm F(x) của hàm số f ( x ) = 3 + cos 4 πx 4 , F ( 4 ) = 2
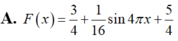
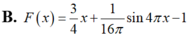
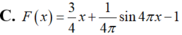
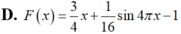
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số y = 3 x - 2 5 - x là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
y
=
3
x
2
-
2
x
+
5
x
2
+
x
+
7
tính nguyên hàm của hàm số f(x)=\(\dfrac{2x+1}{x^4+2x^3+x^2}\)
Câu 1: Tìm giá trị thực của tham số m để hàm số
y= \(\dfrac{1}{3}x^3-mx^{2^{ }}+\left(m^2-4\right)x+3\) tại x=3
Câu 2:Tìm m để hàm số \(y=x^3-2mx^2+mx+1\) đạt cực tiểu tại x=1
Cho hàm số y= f( x) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 Số điểm cực trị của hàm số f x là
A. 5
B. 3
C. 1
D. 2
Tìm khẳng định sai trong các khẳng định sau đây:
A. Hàm số y = 4cosx - 5 sin 2 x - 3 là hàm số chẵn;
B. Đồ thị hàm số sau có hai tiệm cận đứng y = 3 x 2 - 2 x + 5 x 2 + x - 7
C. Hàm số y = 3 x - 2 3 x + 4 luôn nghịch biến;
D. Hàm số f x = - 2 x với x ≥ 0 sin x 3 với x < 0
không có đạo hàm tại x = 0.
Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính 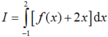 , biết F(-1) = 1, F(2) = 4.
, biết F(-1) = 1, F(2) = 4.
A. I = 6.
B. I = 10.
C. I = 3.
D. I = 9.