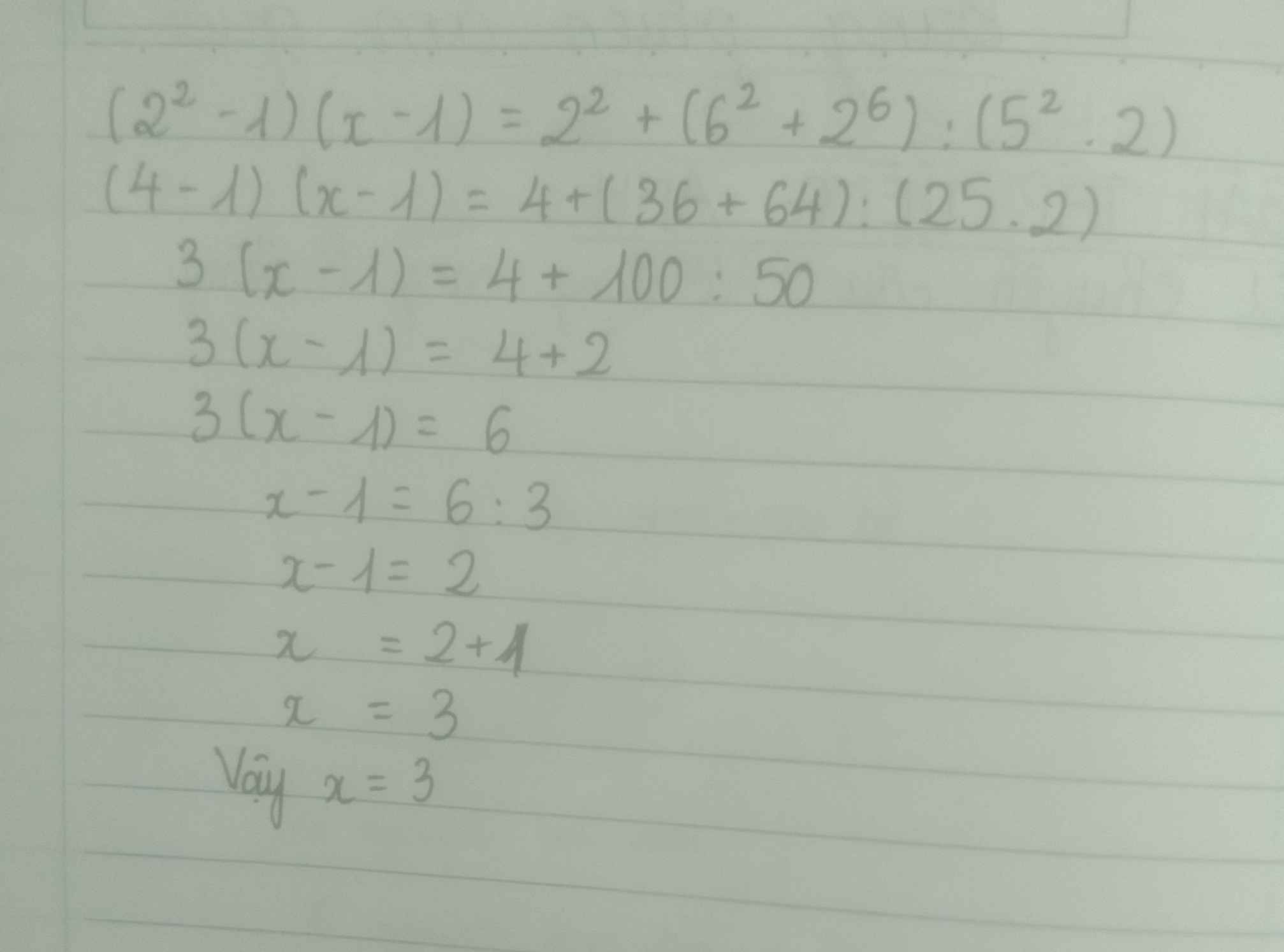1C

2A

1C        2A

Bài 1: 

a) Ta có: \(\dfrac{17}{6}-x\left(x-\dfrac{7}{6}\right)=\dfrac{7}{4}\)

\(\Leftrightarrow\dfrac{17}{6}-x^2+\dfrac{7}{6}x-\dfrac{7}{4}=0\)

\(\Leftrightarrow-x^2+\dfrac{7}{6}x+\dfrac{13}{12}=0\)

\(\Leftrightarrow-12x^2+14x+13=0\)

\(\Delta=14^2-4\cdot\left(-12\right)\cdot13=196+624=820\)

Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{14-2\sqrt{205}}{-24}=\dfrac{-7+\sqrt{205}}{12}\\x_2=\dfrac{14+2\sqrt{2015}}{-24}=\dfrac{-7-\sqrt{205}}{12}\end{matrix}\right.\)

b) Ta có: \(\dfrac{3}{35}-\left(\dfrac{3}{5}-x\right)=\dfrac{2}{7}\)

\(\Leftrightarrow\dfrac{3}{5}-x=\dfrac{3}{35}-\dfrac{10}{35}=\dfrac{-7}{35}=\dfrac{-1}{5}\)

hay \(x=\dfrac{3}{5}-\dfrac{-1}{5}=\dfrac{3}{5}+\dfrac{1}{5}=\dfrac{4}{5}\)

ai giúp mik vs

Bài 3: 

a) Ta có: \(2x-3=x+\dfrac{1}{2}\)

\(\Leftrightarrow2x-x=\dfrac{1}{2}+3\)

\(\Leftrightarrow x=\dfrac{7}{2}\)

b) Ta có: \(4x-\left(x+\dfrac{1}{2}\right)=2x-\left(\dfrac{1}{2}-5\right)\)

\(\Leftrightarrow3x-\dfrac{1}{2}-2x+\dfrac{1}{2}-5=0\)

\(\Leftrightarrow x=5\)

1.

$x(x+2)(x+4)(x+6)+8$

$=x(x+6)(x+2)(x+4)+8=(x^2+6x)(x^2+6x+8)+8$

$=a(a+8)+8$ (đặt $x^2+6x=a$)

$=a^2+8a+8=(a+4)^2-8=(x^2+6x+4)^2-8\geq -8$

Vậy $A_{\min}=-8$ khi $x^2+6x+4=0\Leftrightarrow x=-3\pm \sqrt{5}$

2.

$B=5+(1-x)(x+2)(x+3)(x+6)=5-(x-1)(x+6)(x+2)(x+3)$

$=5-(x^2+5x-6)(x^2+5x+6)$

$=5-[(x^2+5x)^2-6^2]$

$=41-(x^2+5x)^2\leq 41$

Vậy $B_{\max}=41$. Giá trị này đạt tại $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$

3.

Đặt $x+3=a; 7-x=b$ thì $a+b=10$ 

$C=a^4+b^4$

Áp dụng BĐT Bunhiacopxky:

$(a^4+b^4)(1+1)\geq (a^2+b^2)^2$

$\Rightarrow C\geq \frac{(a^2+b^2)^2}{2}$
$(a^2+b^2)(1+1)\geq (a+b)^2=100$

$\Rightarrow a^2+b^2\geq 50$

$\Rightarrow C\geq \frac{50^2}{2}=1250$

Vậy $C_{\min}=1250$

Giá trị này đạt tại $a=b=5\Leftrightarrow x=2$

a) \(\left(x+1\right)^3-\left(x-1\right)^3-6\cdot\left(x-1\right)^2=10\)

\(\Rightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6\cdot\left(x^2-2x+1\right)=10\)

\(\Rightarrow6x^2+2-6x^2+12x-6=10\)

\(\Rightarrow12x-4=10\)

\(\Rightarrow12x=14\)

\(\Rightarrow x=\dfrac{7}{6}\)

b) \(x\left(x+5\right)\left(x-5\right)-\left(x+2\right)\left(x^2-2x+4\right)=42\)

\(\Rightarrow x\left(x^2-25\right)-\left(x^3+8\right)=42\)

\(\Rightarrow x^3-25x-x^3-8=42\)

\(\Rightarrow-25x-8=42\)

\(\Rightarrow-25x=50\)

\(\Rightarrow x=\dfrac{50}{-25}=-2\)

c) \(\left(x-2\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+6\left(x+1\right)^2=49\)

\(\Rightarrow x^3-6x^2+12x-8-\left(x^3-27\right)+6\left(x^2+2x+1\right)=49\)

\(\Rightarrow x^3-6x^2+12x-8-x^3+27+6x^2+12x+6=49\)

\(\Rightarrow24x+25=49\)

\(\Rightarrow24x=24\)

\(\Rightarrow x=\dfrac{24}{24}=1\)

Ta có: \(\left(2^2-1\right)\left(x-1\right)=2^2+\left(6^2+2^6\right):\left(5^2\cdot2\right)\)

\(\Leftrightarrow3\left(x-1\right)=4+2=6\)

\(\Leftrightarrow x-1=2\)

hay x=3

\(\Leftrightarrow6\left(x^2-x-6\right)-3\left(x^2-4x+4\right)-3\left(x^2-1\right)=1\)

\(\Leftrightarrow6x^2-6x-36-3x^2+12x-12-3x^2+3=1\)

\(\Leftrightarrow6x=46\)

hay x=23/3