Cho hình vẽ dưới đây. Tính x và y biết a // b
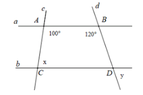
A. x = 80 o ; y = 80 o
B. x = 60 o ; y = 80 o
C. x = 80 o ; y = 60 o
D. x = 60 o ; y = 60 o
Cho hình vẽ dưới đây, biết a ∥ b . Tính x;y
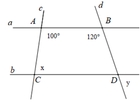
A. x = 80 ° ; y = 80 °
B. x = 60 ° ; y = 80 °
C. x = 80 ° ; y = 60 °
D. x = 60 ° ; y = 60 °
Cho hình vẽ dưới đây, biết AB // CD. Tính x, y
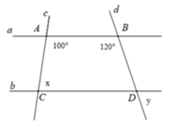
A. x = 80° ; y = 80°
B. x = 60° ; y = 80°
C. x = 80° ; y = 60°
D. x = 60° ; y = 60°
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị (C): y=f(x), trục hoành và hai đường thẳng x=a, y=b (như hình vẽ dưới đây). Giả sử S D là diện tích của hình phẳng D. Chọn công thức đúng trong các phương án dưới đây
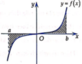
A. S D = − ∫ a 0 f x d x + ∫ 0 b f x d x .
B. S D = ∫ a 0 f x d x − ∫ 0 b f x d x .
C. S D = ∫ a 0 f x d x + ∫ 0 b f x d x .
D. S D = − ∫ a 0 f x d x − ∫ 0 b f x d x .
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị (C): y=f(x), trục hoành và hai đường thẳng x=a, y=b (như hình vẽ dưới đây). Giả sử S D là diện tích của hình phẳng D. Chọn công thức đúng trong các phương án dưới đây
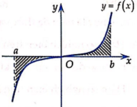
A. S D = − ∫ a 0 f x d x + ∫ 0 b f x d x .
B. S D = ∫ a 0 f x d x − ∫ 0 b f x d x .
C. S D = ∫ a 0 f x d x + ∫ 0 b f x d x .
D. S D = − ∫ a 0 f x d x − ∫ 0 b f x d x .
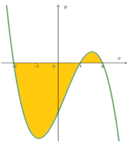
Cho đồ thị y=f(x) như hình vẽ sau đây. Biết rằng ∫ - 2 1 f ( x ) d x = a và ∫ 1 2 f ( x ) d x = b . Tính diện tích S của phần hình phẳng được tô đậm.
![]()
![]()
![]()
![]()
Cho đồ thị y=f(x) như hình vẽ sau đây. Biết rằng ∫ - 2 1 f ( x ) d x = a và ∫ 1 2 f ( x ) d x = b . Tính diện tích S của phần hình phẳng được tô đậm
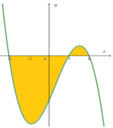
A. S=b-a
B. S=-a-b
C. S=a-b
D. S=a+b
Chọn đáp án A
Phương pháp
Sử dụng công thức tính diện tích mặt phẳng giới hạn bởi đồ thị hàm số y=f(x), trục Ox và hai đường thẳng x=a,x=b là
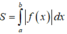
Chú ý đến dấu của f(x) khi phá dấu giá trị tuyệt đối. Nếu đồ thị nằm dưới Ox thì f(x)<0, nếu đồ thị nằm trên Ox thì f(x)>0.
Cách giải
Trên (-2;1) thì đồ thị nằm phía dưới Ox nên f(x)<0, trên khoảng (1;2) thì đồ thị nằm trên Ox nên f(x)>0
Nên từ hình vẽ ta có diện tích phần được tô đậm là
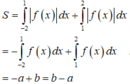
Cho hai hàm số f(x) và g(x) có đồ thị như hình vẽ dưới đây
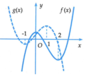
Biết rằng hai hàm số y = f - 2 x + 1 và y = 3 g a x + b a , b ∈ Q có cùng khoảng đồng biến. Giá trị của biểu thức a + 2 b bằng
A. a + 2 b = 3
B. a + 2 b = 4
C. a + 2 b = 2
D. a + 2 b = 6
Cho hàm số
y
=
f
x
=
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
∈
ℝ
,
a
≠
0
có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y = f '(x) cho bởi hình vẽ dưới đây.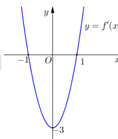 Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
A. S = 9
B. S = 5 4
C. S = 21 4
D. S = 27 4
Đáp án D
Dựa vào đồ thị hàm số y = f ' ( x ) ⇒ f ' x = 3 x 2 - 1
Khi đó f x = ∫ f ' x d x = x 3 - 3 x + C .
Điều kiện đồ thị hàm số f(x) tiếp xúc với đường thẳng y = 4 là:
f x = 4 f x = 0 ⇒ x 3 - 3 x + C = 4 3 x 2 - 1 = 0 ⇔ x = - 1 C = 2 (Do x < 0 suy ra f x = x 3 - 3 x + 2 C
Cho C ∩ O x ⇒ hoành độ các giao điểm là x = -2,x = 1
Khi đó S = ∫ - 2 1 x 3 - 3 x + 2 d x = 27 4 .
Cho hình vẽ dưới đây, trong đó a//b. Tính số đo x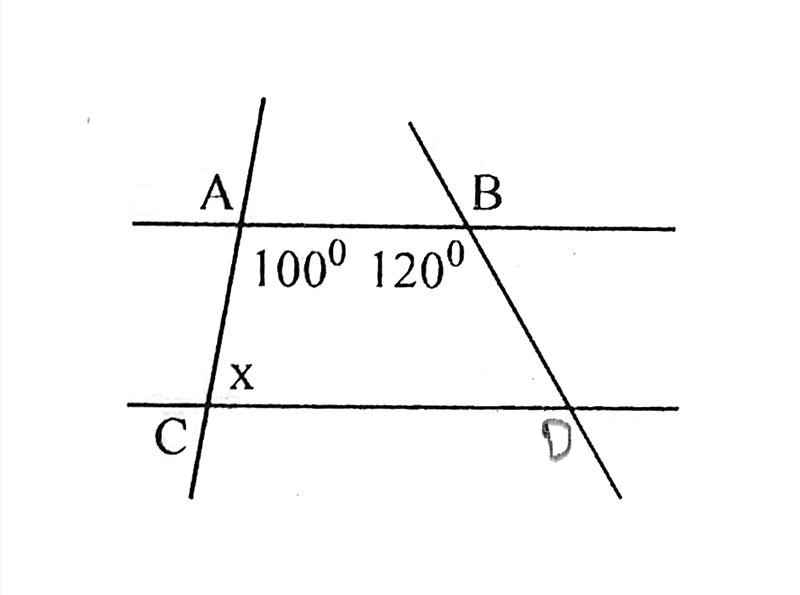
Lời giải:
Vì $AB\parallel CD$ nên $100^0+x=180^0$ (hai góc trong cùng phía)
$x=180^0-100^0=80^0$
Ta có: AB//CD(gt)
nên \(\widehat{BAC}+x=180^0\)(hai góc trong cùng phía)
hay \(x=80^0\)