Cho hàm số y=f(x) liên tục trên R và hàm số y = g ( x ) = x f ( x 2 )  có đồ thị trên đoạn [0; 2] như hình vẽ bên. Biết diện tích S của miền được tô đậm bằng 5/2, tính tích phân  I = ∫ 1 4 f ( x ) d x

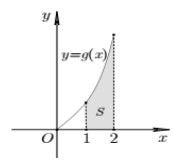
A. 5/4

B. 5/2

C. 5

D. 10

Cho hàm số y=f(x)  liên tuc trên R và thỏa mãn  f(0)<0<f(-1) Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f x ,   y = 0 , x = − 1   v à   x = 1.  Xét các mênh đề sau

1.    S = ∫ − 1 0 f x d x + ∫ 0 1 f x d x              2.    S = ∫ − 1 1 f x d x             3.    S = ∫ − 1 1 f x d x              4.    S = ∫ − 1 1 f x d x  

Số mệnh đề đúng là

A. 2 

B. 1

C. 3

D. 4

Cho hàm số y = f(x)  liên tục trên R  và hàm số y   = g ( x )   =   x f ( x 2 )   có đồ thị trên đoạn [1;2]  như hình vẽ bên. Biết phần diện tích miền được tô màu là S = 5/2 , tính tích phân  I   =   ∫ 1 4 f ( x ) d x

A. I = 7

B. I = 6

C. I = 10

D. I = 5

Cho hàm số y = f(x) liên tục trên R và hàm số y = g(x) = x.f(x²) có đồ thị trên đoạn [0;2] như hình vẽ bên. Biết diện tích S của miền được tô đậm bằng 5/2 tính tích phân  I   =   ∫ 1 4 f ( x ) d x

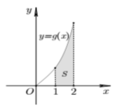
A. I = 5/4

B. I = 5/2

C. I = 5

D. I = 10

Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:

a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)

b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)

Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:

a) \(y=f(2-3x)\)

b) \(y=f(x^2+1)\)

c) \(y=f(3x+1)\)

Cho hàm số y=f(x) xác định và có đạo hàm trên đoạn [0;2]. Biết rằng f(2)=-3 và ∫ 0 2 x f ' ( x ) d x = - 4 . Tính tích phân ∫ 0 2 f ( x ) d x

A. -1 

B. 0 

C. -7 

D. -2