Tìm giá trị lớn nhất của hàm số y = c o s 2 x + s i n x + 3 trên R.
A. m a x R y = 4
B. m a x R y = 5
C. m a x R y = 15 4
D. m a x R y = 17 4
Những câu hỏi liên quan
20 tháng 7 2023 lúc 11:14
Cho hàm số \(y=f\left(x\right)=x^2+6x+5\). Gọi \(m,M\) lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y=f\left(f\left(x\right)\right)\) với \(x\in\left[-3;0\right]\). Tính tổng \(S=m+M.\)
Ta có:
Khi \(x\in\left[-3;0\right]\) thì \(f\left(x\right)\in\left[-4;5\right]\) (dùng BBT)
Lại có:
\(y=f\left(f\left(x\right)\right)=f^2\left(x\right)+6f\left(x\right)+5\)
Khi \(f\left(x\right)\in\left[-4;5\right]\) thì \(f\left(f\left(x\right)\right)\in\left[-4;60\right]\) (dùng BBT)
Do đó, \(m=-4\Leftrightarrow f\left(x\right)=-3\Leftrightarrow x=-2\)
và \(M=60\Leftrightarrow f\left(x\right)=5\Leftrightarrow x=0\)
\(\Rightarrow S=m+M=-4+60=56\)
Đúng 2
Bình luận (0)
Cho hàm số y 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x
∈
[−3; 4] A.
max
−
3
;
4
y
4
B.
min
y
−
2
−
3...
Đọc tiếp
Cho hàm số y = 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x ∈ [−3; 4]
A. max − 3 ; 4 y = 4
B. min y = − 2 − 3 ; 4
C. Cả A, B đều đúng
D. Cả A, B đều sai
Tìm giá trị lớn nhất, giá trị lớn nhất của hàm số (nếu có)
a, \(y=\sqrt{x^2+x-2}\)
b, \(y=\sqrt{2+x}+\sqrt{4-x}\)
c, \(y=x+\sqrt{4-x^2}\)
Lời giải:
a. $y=\sqrt{x^2+x-2}\geq 0$ (tính chất cbh số học)
Vậy $y_{\min}=0$. Giá trị này đạt tại $x^2+x-2=0\Leftrightarrow x=1$ hoặc $x=-2$
b.
$y^2=6+2\sqrt{(2+x)(4-x)}\geq 6$ do $2\sqrt{(2+x)(4-x)}\geq 0$ theo tính chất căn bậc hai số học
$\Rightarrow y\geq \sqrt{6}$ (do $y$ không âm)
Vậy $y_{\min}=\sqrt{6}$ khi $x=-2$ hoặc $x=4$
$y^2=(\sqrt{2+x}+\sqrt{4-x})^2\leq (2+x+4-x)(1+1)=12$ theo BĐT Bunhiacopxky
$\Rightarrow y\leq \sqrt{12}=2\sqrt{3}$
Vậy $y_{\max}=2\sqrt{3}$ khi $2+x=4-x\Leftrightarrow x=1$
c. ĐKXĐ: $-2\leq x\leq 2$
$y^2=(x+\sqrt{4-x^2})^2\leq (x^2+4-x^2)(1+1)$ theo BĐT Bunhiacopxky
$\Leftrightarrow y^2\leq 8$
$\Leftrightarrow y\leq 2\sqrt{2}$
Vậy $y_{\max}=2\sqrt{2}$ khi $x=\sqrt{2}$
Mặt khác:
$x\geq -2$
$\sqrt{4-x^2}\geq 0$
$\Rightarrow y\geq -2$
Vậy $y_{\min}=-2$ khi $x=-2$
Đúng 1
Bình luận (0)
1/ cho \(^{5x^2+y^2+4xy+4x+4y-1=0}\)
tìm giá trị lớn nhất của S=2x+y-2 và giá trị x,y
2/cho \(x^2+2xy+7.\left(x+y\right)+2y^2+10=0\)
tìm giá trị lớn nhất của S=x+y+1 và giá trị x,y
3/ cho \(3x^2+y^2+2xy+4=7x+3y\)
tìm giá trị lớn nhất của S=x+y+1
Cho hàm số yf(x),
x
∈
-
2
;
3
có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn
-
2
;
3
. Giá trị của SM+m là: A. 6 B. 3 C. 5 D. 1
Đọc tiếp
Cho hàm số y=f(x), x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn - 2 ; 3 . Giá trị của S=M+m là:
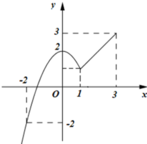
A. 6
B. 3
C. 5
D. 1
Cho hàm số y f(x) có đồ thị như hình vẽ bên. Biết S là tập các giá trị thực của m để hàm số
y
2
f
(
x
)
+
m
có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tính tổng T a + b. A. T 2 B. T 1 C. T -1 D. T -2
Đọc tiếp
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Biết S là tập các giá trị thực của m để hàm số y = 2 f ( x ) + m có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tính tổng T = a + b.
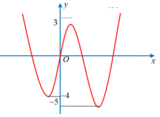
A. T = 2
B. T = 1
C. T = -1
D. T = -2
Đáp án A
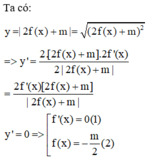
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy
Đúng 0
Bình luận (0)
Gọi S là tập tất cả các giá trị nguyên của m để giá trị lớn nhất của hàm số y
sin
x
+
m
3
-
2
sin
x
thuộc đoạn [-2;2]. Khi đó số phần tử của S là A. 11 B. 10 C. Vô số D. 9
Đọc tiếp
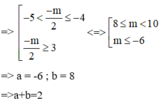
Gọi S là tập tất cả các giá trị nguyên của m để giá trị lớn nhất của hàm số y = sin x + m 3 - 2 sin x thuộc đoạn [-2;2]. Khi đó số phần tử của S là
A. 11
B. 10
C. Vô số
D. 9
Chọn A
Đặt 
ta có: 
Ta có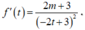 
Do m ∈ Z nên ta xét hai trường hợp sau
+TH1: 
thì hàm số đồng biến trên [-1;1].
Xét 
+TH2: 
thì hàm số nghịch biến trên [-1;1]
Xét 
Vậy 
Vậy tập S có 4 phần tử.
Nên chọn A.
Nhận xét của Admin tổ 4:
Cách khác liên quan đến bản chất Max, Min của hàm số:
Để giá trị lớn nhất của hàm số y = sin x + m 3 - 2 sin x thuộc đoạn [-2;2]
Đúng 0
Bình luận (0)
Cho hàm số
y
1
3
x
3
+
m
2
x
−
2
m
2
+
2
m
−
9
, m là tham số. Gọi S là tất cả các giá trị của m sao cho giá trị lớn nhất của hàm số trên đoạn
0
;
3
không vượt quá 3. Tìm S?. A. ...
Đọc tiếp
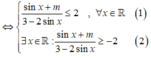
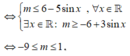
Cho hàm số y = 1 3 x 3 + m 2 x − 2 m 2 + 2 m − 9 , m là tham số. Gọi S là tất cả các giá trị của m sao cho giá trị lớn nhất của hàm số trên đoạn 0 ; 3 không vượt quá 3. Tìm S?.
A. S = − ∞ ; − 3 ∪ 1 ; + ∞
B. S = − 3 ; 1
C. S = − ∞ ; − 3 ∪ 1 ; + ∞
D. S = − 3 ; 1
Đáp án B
Ta có: y ' = x 2 + m 2 ≥ 0 ∀ x ∈ 0 ; 3
Do đó hàm số đồng biến trên đoạn 0 ; 3
Khi đó M ax 0 ; 3 y = y 3 = 9 + 3 m 2 − 2 m 2 + 2 m − 9 = m 2 + 2 m ≤ 3 ⇔ − 3 ≤ m ≤ 1
Đúng 0
Bình luận (0)
a)Tìm giá trị nhỏ nhất của biểu thức:A=lx-11l+l8-yl-19 với x,y cZ
b)Tìm giá trị lớn nhất của biểu thức:A=-(x-9)2+22 với x c Z
Cho hàm số f(x)(2
x
+m)/(√x+1) với m là tham số thực, m1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là A. 1 B. 3 C. 0 D. 2
Đọc tiếp
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
