Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết AC' = a 3

A .   V   =   a 3

B .   V   =   a 3 4

C .   V   =   3 6 a 3 4

D .   V   =   3 3 a 3

Tính thể tích V của khối lập phương ABCD.A'B'C'D' biết đường chéo AC'=a 3 .

A.  a 3 3

B.  3 3 a 3

C.  3 6 a 3 4  

D.  a 3  

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a , điểm M là trung điểm cạnh BC và I là tâm hình vuông CDD'C' . Mặt phẳng (AMI ) chia khối lập phương thành hai khối đa diện, trong đó khối đa diện không chứa điểm D có thể tích là V . Khi đó giá trị của V là

A. \(\frac{7}{36}\)a³ B. \(\frac{22}{29}\)a³ C. \(\frac{7}{29}\)a³ D. \(\frac{29}{36}\)a³

Cho hình hộp chữ nhật ABCD.A′B′C′D′ có A B = a , A A ' = 2 a .  Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là 9 π 2 a 3 . Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′.

A. 4 a 3

B.  4 a 3 3

C.  2 a 3

D.  2 a 3 3

Cho lăng trụ ABCD.A'B'C'D' có ABCD là hình chữ nhật A'A=A'B=A'D. Tính thể tích khối lăng trụ ABCD.A'B'C'D' biết AB= a , AD= a\(\sqrt{ }\)3, AA'=2a

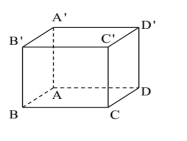A.3a³     B.a³   C.a³\(\sqrt{ }\) 3  D.3a³\(\sqrt{ }\)3

Giúp mk với mình cần gấp ạ

Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là hình vuông cạnh bằng 4cm, đường chéo AB′ của mặt bên (ABB′A′) có độ dài bằng 5cm. Tính thể tích V của khối lăng trụ ABCD.A′B′C′D′.

A. 48 cm 3

B.  24 cm 3

C.  16 cm 3

D.  32 cm 3

Cho hình lập phương ABCD.A' B' C' D' có A'C = 3 a 3 . Thể tích của khối lập phương ABCD.A' B' C' D' là

A.  9 a 3 3

B. 27 a 3

C. 3 a 3

D.  a 3

Một khối lập phương có cạnh a=20cm a, Tính V của khối lập phương đó b, Khối lập phương làm bằng sắt . Tính khối lượng của khối lập phương biết D sắt là 7800kg/m^3

c, Bây h người ta khoét một lỗ trên khối lập phương có V là 4dm^3, rồi lấp đầy vào đó một chất cs khối lượng riêng là 2000kg/m^3. Tìm khối lượng riêng của khối lập phương lúc này