Cho cấp số nhân (un) có các số hạng khác không, tìm u 1 biết:
u 1 + u 2 + u 3 + u 4 + u 5 = 11 u 1 + u 5 = 82 11
A. 1 11
B. 81 11
C. 21 11
D. Tất cả sai
Những câu hỏi liên quan
Cho cấp số nhân (un) có các số hạng khác không, tìm
u
1
biết:
8
u
2
+
5
5
u
5
0...
Đọc tiếp
Cho cấp số nhân (un) có các số hạng khác không, tìm u 1 biết:
8 u 2 + 5 5 u 5 = 0 u 1 3 + u 3 3 = 189
A. 1 hoặc 5
B.5 hoặc 8
C.5
D.1 hoặc 8
Cho cấp số nhân (un) có các số hạng khác không, tìm
u
1
biết:
u
1
+
u
2
+
u
3
+
u
4...
Đọc tiếp
Cho cấp số nhân (un) có các số hạng khác không, tìm u 1 biết:
u 1 + u 2 + u 3 + u 4 = 15 u 1 2 + u 2 2 + u 3 2 + u 4 2 = 85
A. 1 hoặc 2
B. 1 hoặc 8
C. 1 hoặc 5
D.5 hoặc 9
Cho cấp số nhân (un) có các số hạng khác không, tìm
u
1
biết:
u
1
+
u
2
+
u
3
+
u
4...
Đọc tiếp
Cho cấp số nhân (un) có các số hạng khác không, tìm u 1 biết:
u 1 + u 2 + u 3 + u 4 = 15 u 1 2 + u 2 2 + u 3 2 + u 4 2 = 85
A. 1 hoặc 8
B.2 hoặc 8
C.1 hoặc 6
D.2 hoặc 6
Cho cấp số cộng (un) có số hạng đầu là u = 1 và công sai d = 1. Tìm n sao cho tổng n số hạng đầu tiên của cấp số cộng đó bằng 3003
Xem chi tiết
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Đúng 2
Bình luận (0)
Cho cấp số nhân
u
n
có tổng
n
số hạng đầu tiên là
S
n
6
n
-
1
. Tìm số hạng thứ năm của cấp số nhân đã cho A. 120005 B. 6840 C. 7775 D. 6480
Đọc tiếp
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số nhân đã cho
A. 120005
B. 6840
C. 7775
D. 6480
Chọn D
Cấp số nhân u n có số hạng đầu u 1 và công bội q
Do S n = 6 n - 1 nên q ≠ 1
Khi đó S n = u 1 ( 1 - q n ) 1 - q = 6 n - 1
Ta có : S 1 = u 1 ( 1 - q ) 1 - q ⇔ u 1 = 5
S 2 = u 1 1 - q 2 1 - q ⇔ q = 6
Vậy u 5 = u 1 . q 4 = 6480
Đúng 0
Bình luận (0)
Cho cấp số nhân
u
n
có tổng n số hạng đầu tiên là
S
n
6
n
-
1
. Tìm số hạng thứ năm của cấp số nhân đã cho. A. 120005 B. 6840 C. 7775 D. 6480
Đọc tiếp
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số nhân đã cho.
A. 120005
B. 6840
C. 7775
D. 6480
Tìm các số hạng của cấp số nhân u n có năm số hạng, biết: u 3 = 3 và u 5 = 27
Ta có: u3 = u1.q2 ; u5 = u1.q5.
Theo đề bài, ta có hệ phương trình :
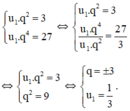
+ Với q = 3 ta có cấp số nhân : 1/3 ; 1 ; 3 ; 9 ; 27.
+ Với q = -3 ta có cấp số nhân : 1/3 ; -1 ; 3 ; -9 ; 27.
Đúng 0
Bình luận (0)
Cho cấp số nhân
(
u
n
)
có tổng n số hạng đầu tiên là
S
n
6
n
-
1
. Tìm số hạng thứ năm của cấp số cộng đã cho A. 6480 B. 6840 C. 7775 D. 12005
Đọc tiếp
Cho cấp số nhân ( u n ) có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số cộng đã cho
A. 6480
B. 6840
C. 7775
D. 12005
Chọn đáp án A
Phương pháp
u 5 = S 5 - S 4
Cách giải
Ta có:
Đúng 0
Bình luận (0)
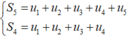
Cho cấp số nhân ( u n ) có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số cộng đã cho
A. 6480
B. 6840
C. 7775
D. 12005
