Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng: G D → . G A → + G D → . G B → + G D → . G C → = 0

Những câu hỏi liên quan
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. chứng minh rằng
D
A
→
+
D
B
→
+
D
C
→
3
D
G
→
Đọc tiếp
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. chứng minh rằng D A → + D B → + D C → = 3 D G →
cho hình tứ diện ABCD. Gọi M là điểm trên cạnh AD sao cho MA = 2MD
a, G là trọng tâm tam giác ABD. Chứng minh rằng: MG // (BCD)
b, H là trọng tâm tam giác ABC. Chứng minh rằng: HG // (BCD)
a: Gọi giao điểm của AG với BC là E
Xét ΔABD có
G là trọng tâm
E là giao điểm của AG với BD
Do đó: E là trung điểm của BD và AG=2/3AE
Xét ΔAHD có \(\dfrac{AG}{AE}=\dfrac{AM}{AD}=\dfrac{2}{3}\)
nên GM//ED
=>GM//BD
mà BD\(\subset\left(BCD\right)\) và GM không thuộc mp(BCD)
nên GM//(BCD)
b: Gọi giao của AH với BC là F
Xét ΔABC có
H là trọng tâm
F là giao điểm của AH với BC
Do đó: F là trung điểm của BC và AH=2/3AF
Xét ΔAGE có \(\dfrac{AH}{AF}=\dfrac{AG}{AE}=\dfrac{2}{3}\)
nên HG//FE
mà \(FE\subset\left(BCD\right)\);HG không thuộc(BCD)
nên HG//(BCD)
Đúng 1
Bình luận (1)
Cho tứ diện ABCD có \(\widehat {CBD} = {90^0}.\)
a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc
BC.
b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng
GK vuông góc với BC.
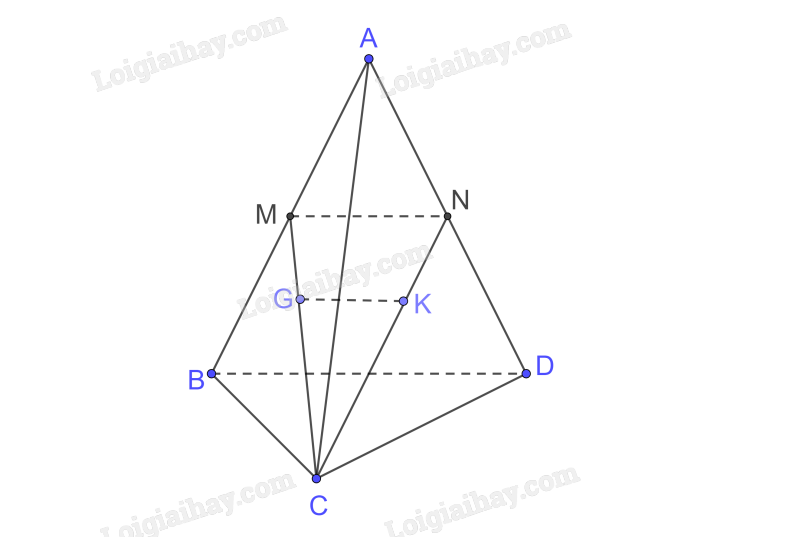
a) Xét tam giác ABD có
M, N tương ứng là trung điểm của AB, AD
\( \Rightarrow \) MN là đường trung bình của tam giác ABD
\( \Rightarrow \) MN // BD mà BD \( \bot \) BC (\(\widehat {CBD} = {90^0}\))
\( \Rightarrow \) MN \( \bot \) BC.
b) Vì G, K tương ứng là trọng tâm của các tam giác ABC, ACD nên \(\frac{{CG}}{{CM}} = \frac{{CK}}{{CN}} = \frac{2}{3}\)
\( \Rightarrow \) GK // MN (Định lý Talet) mà MN \( \bot \) BC
\( \Rightarrow \) GK \( \bot \) BC.
Đúng 0
Bình luận (0)
1. Cho tứ giác ABCD ( AD không song song BC) có E,F lần lượt là trung điểm AD, BC và EFAB+CD/2. Chứng minh rằng tứ giác ABCD là hình thang.2. Cho tứ giác ABCD có ADBC. Đường thẳng đi qua trung điểm M và N của 2 cạnh AB và CD cắt AD và BC lần lượt tại E và F. Chứng minh góc AEMgóc MFB.3. Cho tam giác ABC (ABAC). Trên cạnh AB lấy điểm D sao cho BDAC. Gọi M,N lần lượt là trung điểm của AD, BC. Chứng minh góc BAC 2.BMN4. Cho tứ giác ABCD, gọi A, B, C, D lần lượt là trọng tâm của các tam giác BCD,...
Đọc tiếp
1. Cho tứ giác ABCD ( AD không song song BC) có E,F lần lượt là trung điểm AD, BC và EF=AB+CD/2. Chứng minh rằng tứ giác ABCD là hình thang.
2. Cho tứ giác ABCD có AD=BC. Đường thẳng đi qua trung điểm M và N của 2 cạnh AB và CD cắt AD và BC lần lượt tại E và F. Chứng minh góc AEM=góc MFB.
3. Cho tam giác ABC (AB>AC). Trên cạnh AB lấy điểm D sao cho BD=AC. Gọi M,N lần lượt là trung điểm của AD, BC. Chứng minh góc BAC = 2.BMN
4. Cho tứ giác ABCD, gọi A', B', C', D' lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Chứng minh rằng các đường thẳng AA', BB', CC', DD' đồng quy.
5. Cho tam giác ABC, G là trọng tâm. Đường thẳng d không cắt các cạnh của tam giác ABC. Gọi A', B', C', G' lần lượt là hình chiếu của A, B, C, G trên đường thẳng d. Chứng minh GG'=AA'+BB'+CC'/3
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của hai tam giác ABC và A’B’C’.
a) Chứng minh rằng tứ giác AGG’A’ là hình bình hành.
b) Chứng minh rằng AGC.A’G’C’ là hình lăng trụ.
a) Ta có ABC.A'B'C' là hình lăng trụ nên \(\Delta ABC = \Delta A'B'C'\) suy ra AG = A'G'.
Lại có (ABC) // (A'B'C'), giao tuyến của mp(AGG'A') với (ABC) và (A'B'C') lần lượt là AG, A'G' suy ra AG // A'G'.
Như vậy , tứ giác AGG'A' có AG = A'G', AG // A'G' là hình bình hành.
b) AGG'A' là hình bình hành suy ta AA' // GG'.
Lại có AA' // CC' (do ABC.A'B'C' là hình lăng trụ).
Mặt phẳng (AGC) // (A'G'C') suy ra AGC.A'G'C' là hình lăng trụ.
Đúng 0
Bình luận (0)
Cho tam giác ABC có trung tuyến AM. Lấy điểm G trên AM sao cho AG = 2GM
a) Chứng minh rằng G là trọng tâm của tam giác ABC
b) Gọi D, E, F lần lượt là hính chiếu của G trên các cạnh BC, CA, AB. Chứng minh rằng G cũng là trọng tâm của tam giác DEF
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho BI=2IC. Chứng minh rằng IG song song với mặt phẳng (ACD).
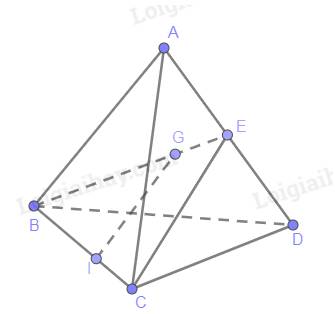
Tam giác BCE có E là trung điểm AD
Suy ra:\(\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}\)
Theo Ta lét, IG //CE
Mà CE thuộc (ACD)
Suy ra: IG // (ACD)
Đúng 0
Bình luận (0)
gọi G là trọng tâm của tứ diện ABCD .
a) chứng minh rằng đường thẳng đi qua G và 1 đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy .
b) gọi A' là trọng tâm của mặt BCD . chứng mình rằng GA=3GA' .
gọi G là trọng tâm của tứ diện ABCD .
a) chứng minh rằng đường thẳng đi qua G và 1 đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy .
b) gọi A' là trọng tâm của mặt BCD . chứng mình rằng GA=3GA' .













