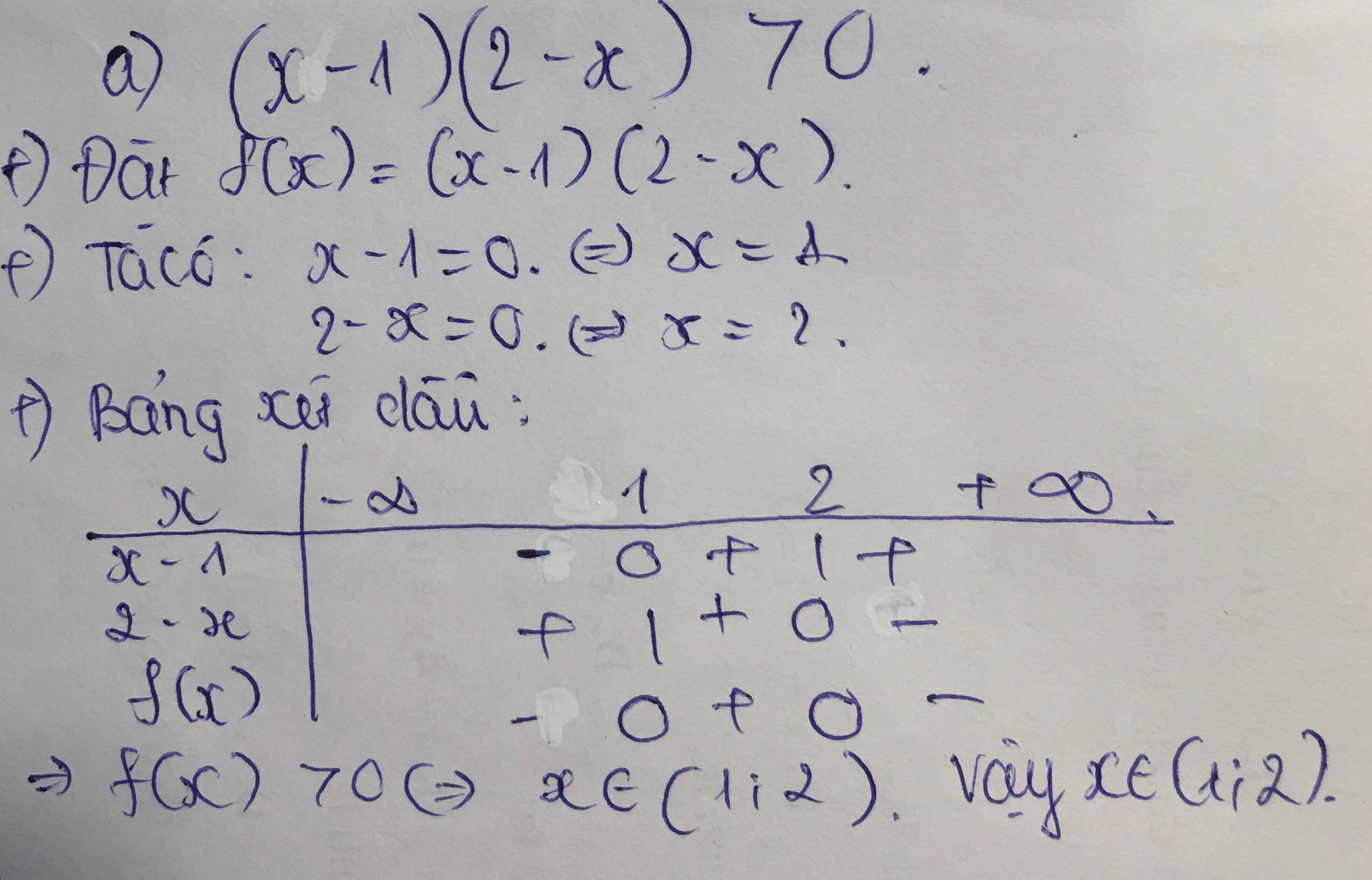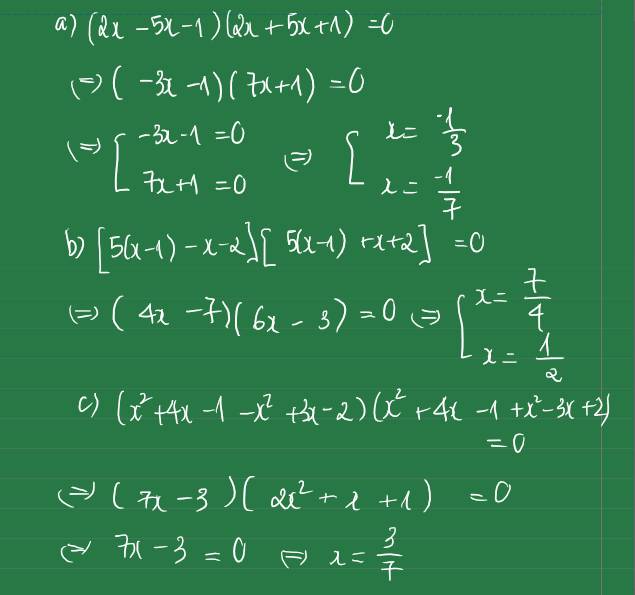3x² + 2x - 1 = 0

=> 3x² + 3x - x - 1 = 0

=> 3x(x + 1) - (x + 1) = 0

=> (3x - 1)(x + 1) = 0

=> \(\orbr{\begin{cases}3x-1=0\\x+1=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=\frac{1}{3}\\x=-1\end{cases}}\)

x² - 5x + 6 = 0

=> x² - 2x - 3x + 6 = 0

=> x(x - 2) - 3(x - 2) = 0

=> (x - 3)(x - 2) = 0

=> \(\orbr{\begin{cases}x-3=0\\x-2=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=3\\x=2\end{cases}}\)

3x² + 7x + 2 = 0

=> 3x² + 6x + x  + 2 = 0

=> 3x(x + 2) + (x + 2) = 0

=> (3x + 1)(x + 2) = 0

=> \(\orbr{\begin{cases}3x+1=0\\x+2=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=-\frac{1}{3}\\x=-2\end{cases}}\)

1, \(3x^2+2x-1=0\Leftrightarrow3x^2+3x-x-1=0\)

\(\Leftrightarrow3x\left(x+1\right)-\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(3x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\3x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{1}{3}\end{cases}}}\)

2, \(x^2-5x+6=0\Leftrightarrow x^2-2x-3x+6=0\)

\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}}\)

3, \(3x^2+7x+2=0\Leftrightarrow3x^2+6x+x+2=0\)

\(\Leftrightarrow3x\left(x+2\right)+\left(x+2\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(3x+1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\3x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-\frac{1}{3}\end{cases}}}\)

\(x^2-4x+1=0\)

\(\Leftrightarrow\left(x^2-4x+4\right)=3\)

\(\Leftrightarrow\left(x-2\right)^2=3\)

\(\Leftrightarrow x=\sqrt{3}+2;x=2-\sqrt{3}\)

\(2x^2-6x+1=0\)

\(\Leftrightarrow4x^2-12x+2=0\)

\(\Leftrightarrow\left(2x-3\right)^2=7\)

\(\Leftrightarrow x=\frac{\sqrt{7}+3}{2};x=\frac{3-\sqrt{7}}{2}\)

\(3x^2+4x-4=0\)

\(\Leftrightarrow3x^2-2x+6x-4=0\)

\(\Leftrightarrow\left(x+2\right)\left(3x-2\right)=0\)

\(\Leftrightarrow x=-2;x=\frac{2}{3}\)

a,Thay m=2 vào pt :

\(\left(1\right)\Leftrightarrow x^2-4x+3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)

b, Để pt có 2 nghiệm thì \(\Delta'\ge0\)

\(\Leftrightarrow\left(-2\right)^2-1\left(m+1\right)\ge0\\ \Leftrightarrow4-m-1\ge0\\ \Leftrightarrow3-m\ge0\\ \Leftrightarrow m\le3\)

Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m+1\end{matrix}\right.\)

\(x^2_1+x^2_2=5\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=5.4\\ \Leftrightarrow4^2-2\left(m+1\right)=20\\ \Leftrightarrow16-2m-2-20=0\\ \Leftrightarrow m=-3\left(tm\right)\)

a)Thay \(m=2\) vào (1) ta đc:

  \(x^2-4x+2+1=0\Rightarrow x^2-4x+3=0\)

  \(\Rightarrow\left(x-3\right)\left(x-1\right)=0\)

  \(\Rightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)

b)Áp dụng hệ thức Viet:

   \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{4}{1}=4\\x_1\cdot x_2=\dfrac{c}{a}=m+1\end{matrix}\right.\) (*)

   Theo bài: \(x_1^2+x^2_2=5\left(x_1+x_2\right)\)

    \(\Rightarrow\left(x_1+x_2\right)^2-2x_1\cdot x_2=5\left(x_1+x_2\right)\)

    \(\Rightarrow4^2-2\cdot\left(m+1\right)=5\cdot4\)

    \(\Rightarrow m=-1\)

a) Khi m = -5 ta được phương trình x 2 + 4x - 5 = 0

Ta có a + b + c = 1 + 4 + (-5) = 0 nên phương trình có hai nghiệm phân biệt là x 1  = 1; x 2  = c/a = (-5)/1 = -5

Tập nghiệm của phương trình S = {1; -5}

Đặt m =  x 2  – 2x

Ta có:  x 2 - 2 x 2  – 2 x 2  + 4x – 3 = 0

⇔  x 2 - 2 x 2  – 2( x 2  – 2x) – 3 = 0

⇔  m 2 – 2m – 3 = 0

Phương trình  m 2  – 2m – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0

Suy ra:  m 1  = -1,  m 2  = 3

Với m = -1 ta có:  x 2 – 2x = -1 ⇔  x 2  – 2x + 1 = 0

Phương trình  x 2  – 2x + 1 = 0 có hệ số a = 1, b = -2, c = 1 nên có dạng a + b + c = 0

Suy ra:  x 1 = x 2  = 1

Với m = 3 ta có:  x 2 – 2x = 3 ⇔  x 2 – 2x – 3 = 0

Phương trình  x 2  – 2x – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0

Suy ra:  x 1  = -1,  x 2 = 3

Vậy phương trình đã cho có 3 nghiệm:  x 1  = 1,  x 2  = -1,  x 3  = 3

a: =>(2x-5x-1)(2x+5x+1)=0

=>(-3x-1)(7x+1)=0

=>x=-1/3 hoặc x=-1/7

b: =>(5x-5)^2-(x+2)^2=0

=>(5x-5-x-2)(5x-5+x+2)=0

=>(4x-7)(6x-3)=0

=>x=1/2 hoặc x=7/4

c: =>(x^2+4x-1-x^2+3x-2)(x^2+4x-1+x^2-3x+2)=0

=>(7x-3)(2x^2+x+1)=0

=>7x-3=0

=>x=3/7

a: =>(5x+3)(x-1)=0

=>x=1 hoặc x=-3/5

b: =>(x-3)(4x-1-5x-2)=0

=>(x-3)(-x-3)=0

=>x=-3 hoặc x=3

c: =>(x+6)(3x-1+x-6)=0

=>(x+6)(4x-7)=0

=>x=7/4 hoặc x=-6