Trong hình 1.4, hãy chỉ ra các vectơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau.
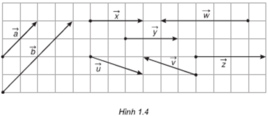
Trong hình 1.4 hãy chỉ ra các vectơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau :
- Các vectơ cùng phương: và
;
,
,
và
;
và
.
- Các vectơ cùng hướng: và
;
,
,
- Các vectơ ngược hướng: và
;
và
;
và
;
và
.
- Các vectơ bằng nhau: =
.
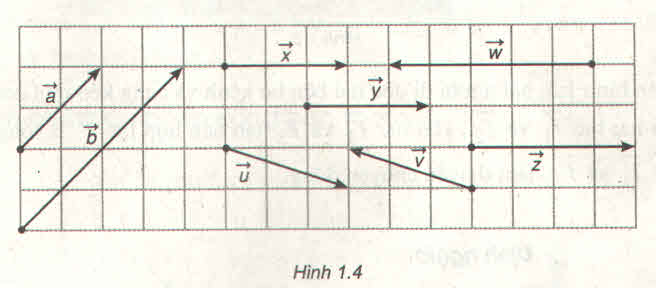
Xét các vectơ cùng phương trong Hình 4.7. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \)được gọi là cùng hướng, còn hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) được gọi là ngược hướng. Hãy chỉ ra các vectơ cùng hướng với vectơ \(\overrightarrow a \) và các vectơ ngược hướng với vectơ \(\overrightarrow a \).
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.
Hãy chỉ ra các cặp vectơ cùng hướng, ngược hướng, bằng nhau trong hình 17.
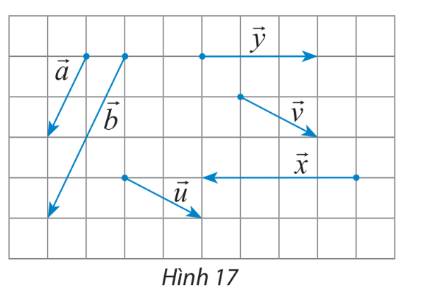
+ Các cặp vectơ cùng hướng là: \(\overrightarrow a \) và \(\overrightarrow b \); \(\overrightarrow u \) và \(\overrightarrow v \)
+ Các cặp vectơ ngược hướng là: \(\overrightarrow x \) và \(\overrightarrow y \)
+ Các cặp vectơ bằng nhau là: \(\overrightarrow u \) và \(\overrightarrow v \)
Trong hình 1.4, hãy chỉ ra các vec tơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau.

– Các vectơ cùng phương: và
;
,
,
và
;
và
.
– Các vectơ cùng hướng: và
;
,
,
– Các vectơ ngược hướng: và
;
và
;
và
;
và
.
– Các vectơ bằng nhau: =
.
Quan sát Hình 8 và gọi tên các vectơ:
a) Cùng phương với vectơ \(\overrightarrow x \);
b) Cùng hướng với vectơ \(\overrightarrow a \) ;
Ngược hướng với vectơ \(\overrightarrow u \).
Quan sát Hình 8 và gọi tên các vectơ:
a) Cùng phương với vectơ \(\overrightarrow x \);
b) Cùng hướng với vectơ \(\overrightarrow a \) ;
Ngược hướng với vectơ \(\overrightarrow u \).
a) Ta có:
Giá của vectơ \(\overrightarrow {\rm{w}} \) trùng với giá của \(\overrightarrow x \)
Giá của vectơ \(\overrightarrow y \), \(\overrightarrow z \)song song với giá của \(\overrightarrow x \)
Suy ra các vectơ cùng phương với vectơ \(\overrightarrow x \) là \(\overrightarrow {\rm{w}} \), \(\overrightarrow y \)và \(\overrightarrow z \)
b) Ta có:
Vectơ \(\overrightarrow b \) có giá song song với vectơ \(\overrightarrow a \)và có cùng hướng từ trên xuống với vectơ \(\overrightarrow a \)nên vectơ \(\overrightarrow b \) cùng hướng với vectơ \(\overrightarrow a \)
c) Ta có:
Vectơ \(\overrightarrow v \) có giá song song với vectơ \(\overrightarrow u \)và ngược hướng từ dưới lên trên so với vectơ \(\overrightarrow u \)nên vectơ \(\overrightarrow v \) ngược hướng với vectơ \(\overrightarrow u \)
Tìm các lực cùng hướng và ngược hướng trong số các lực đẩy được biểu diễn bằng các vectơ trong hình 18.
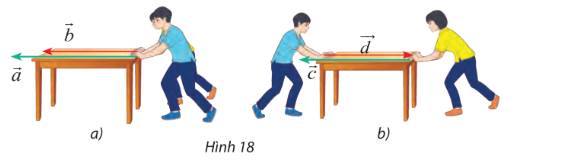
Nhận xét: giá của 4 lực đều song song hoặc trùng nhau, do đó 4 vecto là cùng phương.
Vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) có chiều từ phải sang trái còn vectơ \(\overrightarrow d \) có chiều từ trái sang phải
Vậy các vectơ (hay lực) cùng hướng với nhau là vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \).
Các vectơ (lực) \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) ngược hướng với vectơ \(\overrightarrow d \).
Cho hình bình hành ABCD tâm O. Gọi M và N lần lượt là trung điểm của AD và BC. Dựa vào các điểm A, B, C, D, O, M, N đã cho, hãy :
a) Kể tên hai vectơ cùng phương với \(\overrightarrow{AB}\), hai vectơ cùng hướng với \(\overrightarrow{AB}\), hai vectơ ngược hướng với \(\overrightarrow{AB}\) (các vectơ kể ra này đều khác \(\overrightarrow{0}\)
b) Chỉ ra một vectơ bằng vectơ \(\overrightarrow{MO}\) , một vectơ bằng vectơ \(\overrightarrow{OB}\) ?
a)
Các véc tơ cùng phương với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{OM};\overrightarrow{MN};\overrightarrow{NM};\overrightarrow{NO};\overrightarrow{ON};\overrightarrow{DC};\overrightarrow{CD};\overrightarrow{BA};\overrightarrow{AB}\).
Hai véc tơ cùng hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{ON}\).
Hai véc tơ ngược hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{OM};\overrightarrow{ON}\).
b) Một véc tơ bằng véc tơ \(\overrightarrow{MO}\) là: \(\overrightarrow{ON}\).
Một véc tơ bằng véc tơ \(\overrightarrow{OB}\) là: \(\overrightarrow{DO}\).
Trong Hình 4.12, hãy chỉ ra các vecto cùng phương, các cặp vecto ngược hướng và các cặp vecto bằng nhau.
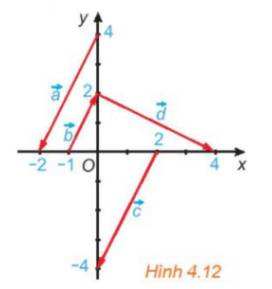
Dễ thấy giá của \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) song song với nhau.
Các vecto cùng phương là: \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)
Trong đó cặp vecto cùng hướng là \(\overrightarrow a ,\overrightarrow c \).
Cặp vecto ngược hướng là: \(\overrightarrow a ,\overrightarrow b \) và \(\overrightarrow b ,\overrightarrow c \).
Cặp vecto bằng nhau là: \(\overrightarrow a ,\overrightarrow c \)