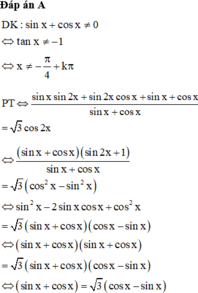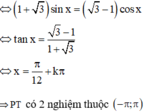Tính: sin 7 π 2 , cos - π 12 , tan 13 π 12
Những câu hỏi liên quan
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Cho sin a = 3/5 với π/2 < a < π Tính sin 2a , cos 2a , tan 2a , cot ( a - π/4 ) , sin a/2 , cos a/2 Cảm ơn trc❤
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Đúng 0
Bình luận (0)
Biết sin a=\(\dfrac{5}{13}\);cos b=\(\dfrac{3}{5}\); \(\dfrac{\text{π}}{2}\)<a<π; 0<b<\(\dfrac{\text{π}}{2}\). Hãy tính sin(a+b)
\(\cos a=\dfrac{-12}{13}\)
\(\sin b=\dfrac{4}{5}\)
\(\sin\left(a+b\right)=\sin a\cos b+\sin b\cos a\)
\(=\dfrac{5}{13}\cdot\dfrac{3}{5}+\dfrac{4}{5}\cdot\dfrac{-12}{13}=\dfrac{-45}{65}=\dfrac{-9}{13}\)
Đúng 1
Bình luận (0)
cho cos a = 3/5, 3π/2 < a < 2π. Tính sin2a, sin(π - π/3)
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow sina< 0\)
\(\Rightarrow sina=-\sqrt{1-cos^2a}=-\sqrt{1-\left(\dfrac{3}{5}\right)^2}=-\dfrac{4}{5}\)
\(\Rightarrow sin2a=2sina.cosa=2.\left(-\dfrac{4}{5}\right).\left(\dfrac{3}{5}\right)=-\dfrac{24}{25}\)
Câu sau có nhầm đề ko nhỉ?
\(sin\left(\pi-\dfrac{\pi}{3}\right)=sin\left(\dfrac{2\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
Đúng 0
Bình luận (0)
Số nghiệm của phương trình
sin
x
.
sin
2
x
+
2
.
sin
x
.
cos
2...
Đọc tiếp
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Sin(x-π/2)+cos(x-π)+tan(5π/2-x)+tan(x-π/2)=-2cosx
\(sin\left(x-\dfrac{\pi}{2}\right)+cos\left(x-\pi\right)+tan\left(\dfrac{5\pi}{2}-x\right)+tan\left(x-\dfrac{\pi}{2}\right)\)
\(=-sin\left(\dfrac{\pi}{2}-x\right)+cos\left(\pi-x\right)+tan\left(2\pi+\dfrac{\pi}{2}-x\right)-tan\left(\dfrac{\pi}{2}-x\right)\)
\(=-cosx-cosx+tan\left(\dfrac{\pi}{2}-x\right)-cotx\)
\(=-2cosx+cotx-cotx=-2cosx\)
Đúng 0
Bình luận (0)
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).
Đúng 0
Bình luận (0)
21 tháng 4 2021 lúc 15:52
Cho \(\sin\alpha=\sqrt{3}\cos\alpha\) và 0 < π < π/2
Tìm \(\sin\alpha,\cos\alpha\)
Chắc là \(0< a< \dfrac{\pi}{2}\)?
\(0< a< \dfrac{\pi}{2}\Rightarrow sina;cosa>0\)
\(\left\{{}\begin{matrix}sina=\sqrt{3}cosa\\sin^2a+cos^2a=1\end{matrix}\right.\) \(\Rightarrow\left(\sqrt{3}cosa\right)^2+cos^2a=1\)
\(\Rightarrow4cos^2a=1\Rightarrow cosa=\dfrac{1}{2}\)
\(\Rightarrow sina=\sqrt{3}cosa=\dfrac{\sqrt{3}}{2}\)
Đúng 2
Bình luận (1)
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
Đúng 2
Bình luận (0)