Gọi A là tập nghiệm của phương trình \({x^2} + x - 2 = 0\),

B là tập nghiệm của phương trình \(2{x^2} + x - 6 = 0\)

Tìm \(C = A \cap B\).

Tìm tập hợp nghiệm của phương trình sau lg(152 + x 3 ) = lg ( x + 2 ) 3

A. {4}              B. {-6}

C. {4;-6}              D. {4;6}

Tìm tập hợp nghiệm của phương trình

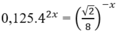
A. {6}              B. {4}

C. {2}              D. {1}

Cho phương trình \(4^x-2^{x+2}+m=0\). Tìm tập hợp tất cả giá trị của tham số \(m\) để phương trình đã cho có hai nghiệm phân biệt

Tìm tập hợp nghiệm của phương trình: 25 x  - 6. 5 x + 1 + 5 3  = 0

A. {1;2}              B. {5;25}

C. {-1;2}              D. {2;-1}

Tìm tập hợp nghiệm của phương trình 2 x 2 - x - 4  = 0

A. {1;2}              B. {2;3}

C. {-2;3}              D. {2;-3}

Tìm tập hợp nghiệm của phương trình log 2  + log 2 ( x - 1 ) = 1

A. {1}              B. {2}

C. {1;2}              D. {-1;2}