Nêu nhận xét về mối liên hệ giữa đồ thị của các hàm số trên Hình 35 và Hình 36.

Những câu hỏi liên quan
Xét hai hàm số \(y = {x^2},y = 2x\) và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp, nêu mối liên hệ của giá trị hàm số tại 1 và -1, 2 và -2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.
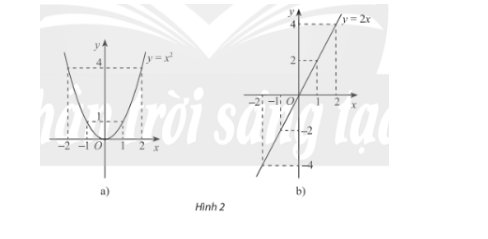
* Hàm số \(y = {x^2}\)
Nhìn đồ thị ta thấy:
+ \(y(1) = y( - 1) = 1,y(2) = y( - 2) = 4\)
+ Đồ thị hàm số đối xứng qua trục Oy.
* Hàm số \(y = 2x\)
Nhìn đồ thị ta thấy:
+ \(y(1) = - y( - 1),y(2) = - y( - 2)\)
+ Đồ thị hàm số đối xứng qua điểm O.
Đúng 0
Bình luận (0)
Quan sát Hình 6.2 và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số ydfrac{1}{2}x^2.�left(0;0right);left(2;2right);left(-2;2right);left(1;2right);left(-1;2right)Nêu nhận xét về mối quan hệ giữa hoành độ và tung độ của những điểm nằm trên đồ thị.
Đọc tiếp
Quan sát Hình 6.2 và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số \(y=\dfrac{1}{2}x^2\).
\(\left(0;0\right);\left(2;2\right);\left(-2;2\right);\left(1;2\right);\left(-1;2\right)\)
Nêu nhận xét về mối quan hệ giữa hoành độ và tung độ của những điểm nằm trên đồ thị.
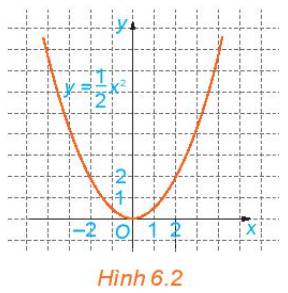
Dựa vào độ thị ta thấy (0; 0); (2; 2); (-2; 2) nằm trên đồ thị hàm số \(y = \frac{1}{2}{x^2}\)
Ta nhận ra được: \(\begin{array}{l}0 = \frac{1}{2}{.0^2}\\2 = \frac{1}{2}{.2^2}\\2 = \frac{1}{2}.{( - 2)^2}\end{array}\) Vì vậy những điểm có tọa độ \(\left( {x;\frac{1}{2}{x^2}} \right)\) sẽ nằm trên đồ thị.
Đúng 0
Bình luận (0)
Tiến hành thí nghiệm 3 và trả lời các câu hỏi:

a) Âm thanh phát ra bởi âm thoa nào nghe bổng hơn?
b) Từ đồ thị dao động âm trên màn hình dao động kí, sóng âm của âm thoa nào phát ra có tần số lớn hơn?
c) Nêu nhận xét về mối liên hệ giữa độ cao của âm với tần số âm.
a) Âm phát ra bởi âm thoa nhỏ hơn nghe bổng nhất.
b) Từ đồ thị dao động âm trên màn hình dao động kí, ta thấy đồ thị dao động âm của âm thoa nhỏ ở sát nhau hơn. Tức là âm thoa nhỏ phát ra tần số lớn hơn.
c) Độ cao của âm liên quan tới tần số. Tần số âm càng lớn thì âm nghe được càng bổng.
Đúng 2
Bình luận (0)
a) âm thoa số 1 phát ra âm bổng hơn
b) âm thoa số 1 có tần số dao động lớn hơn
c) tần số dao động của âm thoa càng lớn thì âm phát ra càng cao (bổng )
Đúng 0
Bình luận (0)
a) Âm phát ra bởi âm thoa nhỏ hơn nghe bổng nhất.
b) Từ đồ thị dao động âm trên màn hình dao động kí, ta thấy đồ thị dao động âm của âm thoa nhỏ ở sát nhau hơn. Tức là âm thoa nhỏ phát ra tần số lớn hơn.
c) Độ cao của âm liên quan tới tần số. Tần số âm càng lớn thì âm nghe được càng bổng.
Đúng 0
Bình luận (0)
Quan sát đồ thị các hàm số: \(y = {x^2} - 4x + 3\) (Hình 14a);
\(y = \frac{{x + 1}}{{x - 1}}\,\,\left( {x \ne 1} \right)\) (Hình 14b);
\(y = \tan x\) (Hình 14c).
Và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.
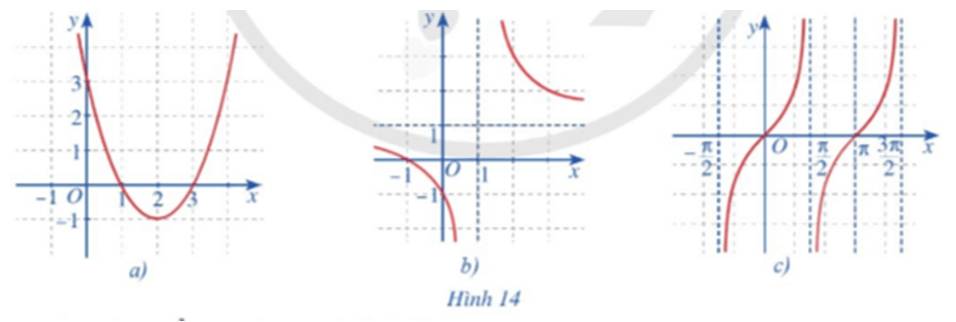
Hình 14a đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ trên khoảng xác định.
Hình 14b đồ thị bị chia làm hai nhánh:
- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.
- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.
Vậy hàm số liên tục trên từng khoảng xác định.
Hình 14c đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.
Đúng 0
Bình luận (0)
2.
a) Dựa vào số liệu đo được từ thí nghiệm hoặc Bảng 23.1, vẽ đồ thị biểu diễn mối liên hệ giữa độ biến dạng của lò xo và lực tác dụng lên lò xo.
b) Nhận xét về hình dạng của đồ thị và rút ra kết luận.
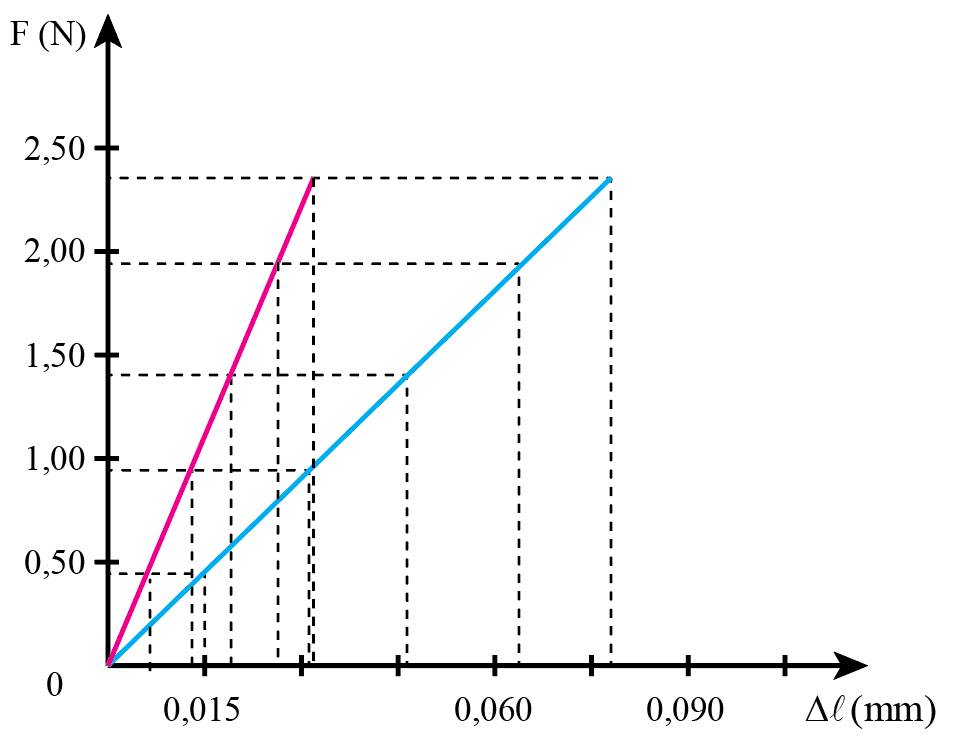
Đồ thị có dạng đường thẳng hướng lên trên, cho thấy lò xo có độ dãn tỉ lệ thuận với lực tác dụng.
Đúng 1
Bình luận (0)
a) Dựa vào số liệu đo được từ thí nghiệm hoặc Bảng 23.1, vẽ đồ thị biểu diễn mối liên hệ giữa độ biến dạng của lò xo và lực tác dụng lên lò xo.
b) Nhận xét về hình dạng của đồ thị và rút ra kết luận.
a) Đồ thị biểu diễn sự phụ thuộc vào lực đàn hồi (trục tung) vào độ biến dạng của lò xo 1 (trục hoành).
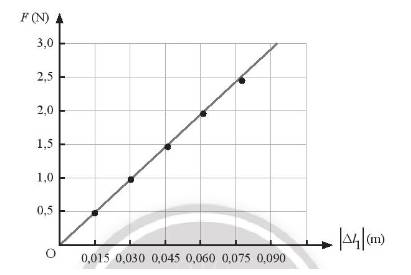
Đồ thị biểu diễn sự phụ thuộc của lực đàn hồi (trục tung) vào độ biến dạng của lò xo 2 (trục hoành).
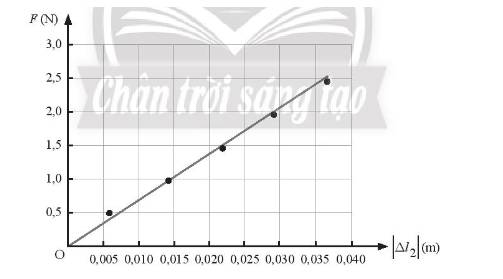
b) Đồ thị có dạng đường thẳng và đi qua gốc tọa độ (đồ thị này được vẽ dựa trên số liệu thí nghiệm được cho trong SGK). Từ đó có thể suy ra được độ lớn lực đàn hồi tỉ lệ thuận với độ biến dạng của lò xo.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
x
+
2
x
2
-
9
có đồ thị như trên hình 53.a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:
x...
Đọc tiếp
Cho hàm số f x = x + 2 x 2 - 9 có đồ thị như trên hình 53.
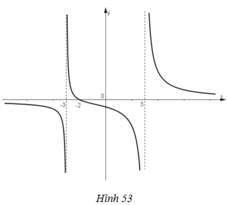
a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:
x → - ∞ , x → 3 - , x → - 3 +
b. Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:

a) Quan sát đồ thị nhận thấy:
f(x) → 0 khi x → -∞
f(x) → -∞ khi x → 3-
f(x) → +∞ khi x → (-3)+.
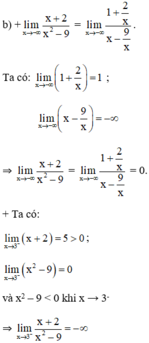
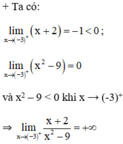
Đúng 0
Bình luận (0)
Nêu tính chất của hàm số mũ, hàm số lôgarit, mối liên hệ giữa đồ thị các hàm số mũ và hàm số lôgarit cùng cơ số ?
1. Tính chất của hàm số mũ y= ax ( a > 0, a# 1).
- Tập xác định: .
- Đạo hàm: ∀x ∈ ,y’= axlna.
- Chiều biến thiên Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
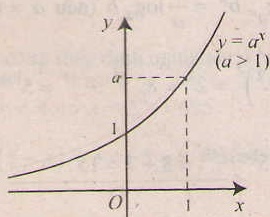
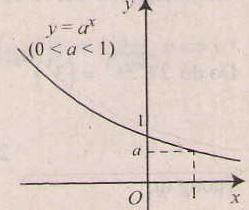
- Tiệm cận: trục Ox là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành ( y= ax > 0, ∀x), và luôn cắt trục tung taih điểm ( 0;1) và đi qua điểm (1;a).
2. Tính chất của hàm số lôgarit y = logax (a> 0, a# 1).
- Tập xác định: (0; +∞).
- Đạo hàm ∀x ∈ (0; +∞),y’ = .
- Chiều biến thiên: Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
- Tiệm cận: Trục Oy là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).
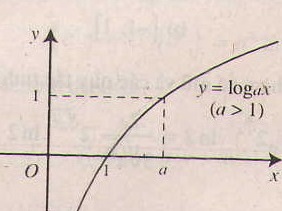
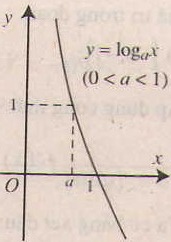
3. Chú ý
- Vì e > 1 nên nếu a > 1 thì lna > 0, suy ra (ax)’ > 0,∀x và (logax)’ > 0, ∀x > 0;
do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.
Tương tự, nếu 0 < a< 1thì lna < 0, (ax)’ < 0 và (logax)’ < 0, ∀x > 0; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.
- Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành
(ln|x|)’ = , ∀x # 0 và (loga|x|)’ =
, ∀x # 0.
Đúng 0
Bình luận (0)
Nêu định nghĩa hàm liên tục tại một điểm, trên một khoảng. Nêu nhận xét về đồ thị của một hàm số liên tục trên một khoảng.
+ Hàm số liên tục tại một điểm

+ Hàm số liên tục trên một khoảng
- Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
- Hàm số y = f(x) được gọi là liên tục trên một đoạn [a; b] nếu nó liên tục tại mọi điểm thuộc khoảng (a;b) và
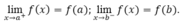
Đồ thị của hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.
Đúng 0
Bình luận (0)


















