a) Quan sát đồ thị nhận thấy:
f(x) → 0 khi x → -∞
f(x) → -∞ khi x → 3-
f(x) → +∞ khi x → (-3)+.
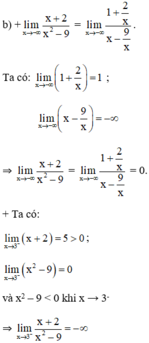
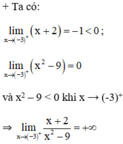
a) Quan sát đồ thị nhận thấy:
f(x) → 0 khi x → -∞
f(x) → -∞ khi x → 3-
f(x) → +∞ khi x → (-3)+.
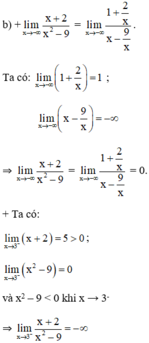
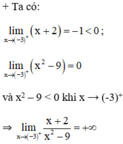
Cho hai hàm số f ( x ) = x 2 và có g x = - x 2 + 2 n ế u x ≤ 1 2 n ế u - 1 < x < 1 - x 2 + 2 n ế u x ≥ 1 đồ thị như hình 55
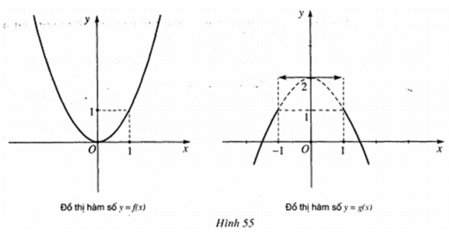
a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1 ;
b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1 .
Cho hàm số f(x) có đồ thị như hình dưới đây:
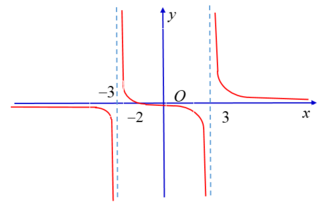
- Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là +∞ ?
A. lim x → - ∞ f x
B. lim x → + ∞ f x
C. lim x → - 3 + f x
D. l i m x → - 3 - f x
Cho hàm số f(x) có đồ thị như hình dưới đây:
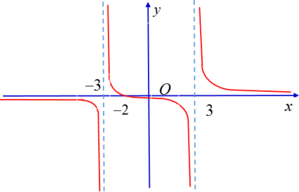
Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là +∞ ?
![]()
![]()
![]()
![]()
Cho hàm số f x = 3 x + 2 n ế u x < - 1 x 2 - 1 n ế u x ≥ - 1
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Cho hàm số f(x)=x+1với x∈R.
a) Giả sử x0∈R.Hàm số f(x)
có liên tục tại điểm x0 hay không?
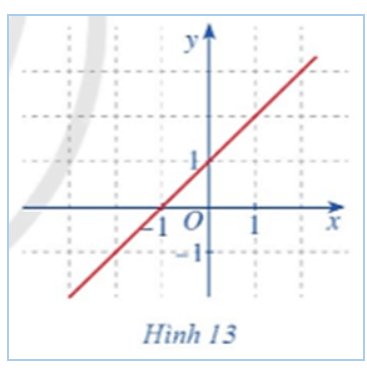
b) Quan sát đồ thị hàm số f(x)=x+1 với x∈R (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
Cho hàm số f(x) có đạo hàm trên ℝ và có đồ thị y=f'(x) như hình vẽ. Xét hàm số g ( x ) = f ( x 2 - 2 ) . Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (-1;0).
B. Hàm số g(x) nghịch biến trên. ( - ∞ ; - 2 )
C. Hàm số g(x) nghịch biến trên. ( 0 ; 2 )
D. Hàm số g(x) đồng biến trên. ( 2 ; + ∞ )
Cho hàm số f ( x ) = 1 / ( x - 2 ) có đồ thị như ở Hình 52
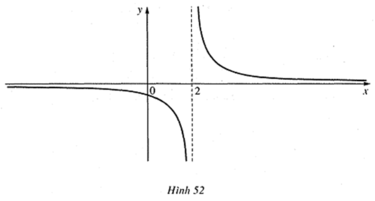
Quan sát đồ thị và cho biết:
- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị nào.
- Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị nào.
Cho hàm số f x = x 2 n ế u x ≥ 0 x 2 - 1 n ế u x < 0
a) Vẽ đồ thị của hàm số f(x). Từ đó dự đoán về giới hạn của f(x) khi x → 0
b) Dùng định nghĩa chứng minh định nghĩa trên
a) Vẽ đồ thị của hàm số f x = x 2 / 2 .
b) Tính f’(1).
c) Vẽ đường thẳng đi qua điểm M(1; 1/2) và có hệ số góc bằng f’(1). Nêu nhận xét về vị trí tương đối của đường thẳng này và đồ thị hàm số đã cho.