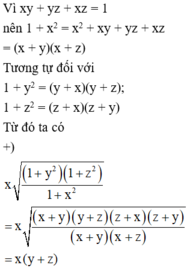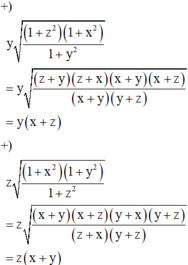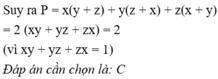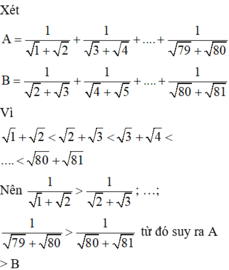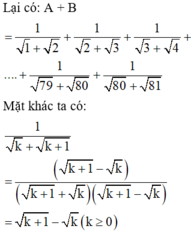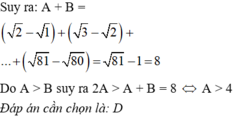0^2020x1^2021x2^2022 x 3^2023x..x21^2120

Những câu hỏi liên quan
Kết quả của phép nhân (x + 2022)(x - 1)là : A.x^2+ 2022x-1 B.x^2+2021x - 2022- C.x^2023x - 2022 D.x^2 - 2021x + 2022 Biểu thức thích hợp là là (a + b) (A^2- AB + B^2) =..... A.A^3 + B^3 B.( A + B)^3 C. A^3 - B^3 D.(A-B)^3
\(1,\left(x+2022\right)\left(x-1\right)=x^2+2021x-2022\left(B\right)\\ 2,\left(a+b\right)\left(a^2-ab+b^2\right)=a^3+b^3\left(A\right)\)
Đúng 0
Bình luận (0)
Tính giá trị biểu thức:
A= x50-2023x49+2023x48-...+2023x2-2023x+2024 tại x = 2022
x=2022
=>x+1=2023
A=x^50-x^49(x+1)+x^48(x+1)-...+x^2(x+1)-x(x+1)+x+2
=x^50-x^50-x^49+x^49+...+x^3+x^2-x^2-x+x+2
=2
Đúng 2
Bình luận (0)
cho:x1+x2+x3+...+x20+x21=0.tinh x21
x1+x2=x3+x4=...=x19+x20=x20+x21=1.tinh x 21
trả lời nhanh nhé,mình đang cần gấp
M=1+(1+2)+(1+2+3)+...+(1+2+3+...+2020)
1 x 2020+2 x 2019+3 x 2018+...+2020x1
Tính M
Ta có: 1 + ( 1 + 2 ) + ( 1 + 2 + 3 ) + ... + ( 1 + 2 + 3 +...+ 2020)
= ( 1 + 1 + 1 +... + 1 ) + (2 + 2 +...+ 2 ) + ( 3 + 3+...+ 3 ) + ...+ 2020
Có 2020 số 1 ; 2019 số 2 ; 2018 số 3 ;... ; 1 số 2020
= 2020 x 1 + 2019 x 2 + 2018 x 3 + ... + 2020x 1
=> \(M=\frac{1+\left(1+2\right)+\left(1+2+3\right)+...+\left(1+2+3+...+2020\right)}{1\times2020+2\times2019+...+2020\times1}\)
= \(\frac{1\times2020+2\times2019+...+2020\times1}{1\times2020+2\times2019+...+2020\times1}=1\)
Tính giá trị biểu thức
P
x
1
+
y
2
1
+
z
2...
Đọc tiếp
Tính giá trị biểu thức P = x 1 + y 2 1 + z 2 1 + x 2 y 1 + z 2 1 + x 2 1 + y 2 z 1 + x 2 1 + y 2 1 + z 2 với x, y, z > 0 và xy + yz + xz = 1.
A. P = 4
B. P = 1
C. P = 2
D. P = 3
Tính giá trị biểu thức
P
x
1
+
y
2
1
+
z
2...
Đọc tiếp
Tính giá trị biểu thức P = x 1 + y 2 1 + z 2 1 + x 2 y 1 + z 2 1 + x 2 1 + y 2 z 1 + x 2 1 + y 2 1 + z 2 với x, y, z > 0 và xy + yz + xz = 1.
A. 1 1 + 2 + 1 3 + 4 + . . . + 1 79 + 80 = 1
B. 1 1 + 2 + 1 3 + 4 + . . . + 1 79 + 80 < 3
C. 1 1 + 2 + 1 3 + 4 + . . . + 1 79 + 80 < 4
D. 1 1 + 2 + 1 3 + 4 + . . . + 1 79 + 80 > 4
Cho x, y, z 0 thỏa mãn xy + yz + zx 1. Tính giá trị của biểu thức
A
x
1
+
y
2
1
+
z
2
1
+
x...
Đọc tiếp
Cho x, y, z > 0 thỏa mãn xy + yz + zx = 1. Tính giá trị của biểu thức
A = x 1 + y 2 1 + z 2 1 + x x + y 1 + z 2 1 + x 2 1 + y 2 + z 1 + x 2 1 + y 2 1 + z 2
A. A = 1
B. A = 3
C. A = 2
D. A = 0
Chọn đáp án C.
Vì x, y ,z > 0 nên x + y > 0; y + z > 0 và x + z > 0
Ta có:
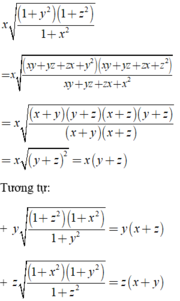
Khi đó
A = x(y + z) + y(x + z) + z(x + y)
= xy + xz + xy + yz + xz + zy = 2(xy + yz + zx) = 2
Đúng 0
Bình luận (0)
phân tích đa thức:
x4 + 2021x2 + 2020x + 2021
a(b2 - c2) + b(c2 - a2) + c(a2 - b2)
a3(b - c) + b3(c - a) + c3(a - b)
(x + y + z)3 - (x + y - z)3 - (x - y + z)3 - (-x + y + z)3
b) Ta có: \(a\left(b^2-c^2\right)+b\left(c^2-a^2\right)+c\left(a^2-b^2\right)\)
\(=ab^2-ac^2+bc^2-ba^2+ca^2-cb^2\)
\(=\left(ab^2-cb^2\right)+\left(ca^2-c^2a\right)+\left(bc^2-ba^2\right)\)
\(=b^2\left(a-c\right)+ca\left(a-c\right)+b\left(c^2-a^2\right)\)
\(=\left(a-c\right)\left(b^2+ca\right)-b\left(a-c\right)\left(a+c\right)\)
\(=\left(a-c\right)\left(b^2+ca-ba-bc\right)\)
\(=\left(a-c\right)\left[b\left(b-a\right)+c\left(a-b\right)\right]\)
\(=\left(a-c\right)\left[b\left(b-a\right)-c\left(b-a\right)\right]\)
\(=\left(a-c\right)\left(b-a\right)\left(b-c\right)\)
Đúng 2
Bình luận (0)
trời ơi cái qq gì í đây
Cho x, y, z thoả mãn xyz = 2023.
Chứng minh: \(\dfrac{2023x}{xy+2023x+2023}+\dfrac{y}{yz+y+2023}+\dfrac{z}{xz+z+1}=1\)
Có `xyz=2023=>2023=xyz`
Thay vào ta có :
\(\dfrac{xyz\cdot x}{xy+xyz\cdot x+xyz}+\dfrac{y}{yz+y+xyz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{x^2yz}{xy\left(1+xz+z\right)}+\dfrac{y}{y\left(z+1+xz\right)}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz}{1+xz+z}+\dfrac{1}{z+1+xz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz+1+z}{1+xz+z}=1\left(dpcm\right)\)
Đúng 1
Bình luận (0)