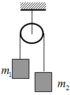
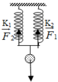
Cho hệ như hình vẽ, m 1 = 1 k g , m 2 = 2 k g . Khối lượng ròng rọc và dây không đáng kể, bỏ qua ma sát.
a. Tính gia tốc chuyển động của hệ vật.
b. Tính sức căng của dây nối, g = 10 m / s 2 .
Cho cơ hệ như hình vẽ. m 1 = 1 k g ; m 2 = 0 , 6 k g ; m 3 = 0 , 2 k g , α = 30 ° . Dây nối m2, m3 dài l = 2 m. Cho g = 10 m / s 2 hệ số ma sát giữa m1 và bàn là 1 10 3 . Tìm gia tốc chuyển động của vật.
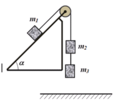
A. 0,54 m / s 2
B. 1,21 m / s 2
C. 1,83 m / s 2
D. 1,39 m / s 2 .
Cho cơ hệ như hình vẽ 1, lò xo lý tưởng có độ cứng k = 100 (N/m) được gắn chặt vào tường tại Q, vật M = 200 (g) được gắn với lò xo bằng một mối nối hàn. Vật M đang ở vị trí cân bằng, một vật m = 50 (g) chuyển động đều theo phương ngang với tốc độ v0 = 2 (m/s) tới va chạm hoàn toàn mềm với vật M. Sau va chạm hai vật dính làm một và dao động điều hòa. Bỏ qua ma sát giữa vật M với mặt phẳng ngang. Viết phương trình dao động của hệ vật? Chọn trục tọa độ như hình vẽ, gốc O trùng tại vị trí cân bằng, gốc thời gian t = 0 lúc xảy ra va chạm.
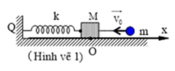
A. x = 4 cos ( 20 t ) ( c m )
B. x = 2 cos ( 20 t + π / 2 ) ( c m )
C. x = 4 cos ( 20 t + π / 2 ) ( c m )
D. x = 2 cos ( 20 t ) ( c m )
Cho con lắc lò xo như hình vẽ. Vật nhỏ khối lượng \(m=200g\), lo xo lí tưởng có độ cứng \(k=1\)N/m góc \(\alpha=30^o\). Lấy g=10m/s2
a/ Chọn trục tọa độ như hình vẽ, gốc tọa độ trùng với vị trí cân bằng. Viết phương trình dao động. Biết tại thời điểm ban đầu lò xo bị dãn 2cm và vật có vận tốc \(v_0=10\sqrt{15}\)cm/s hướng theo chiều dương.
b/ Tại thời điểm t1 lò xo không bị biến dạng, Hỏi tại \(t_2=t_1+\dfrac{\pi}{4\sqrt{5}}s\),vật có tọa độ bao nhiêu?
c/ Tính tốc độ trung bình của m trong khoảng thời gian \(\Delta t=t_2-t_1\)
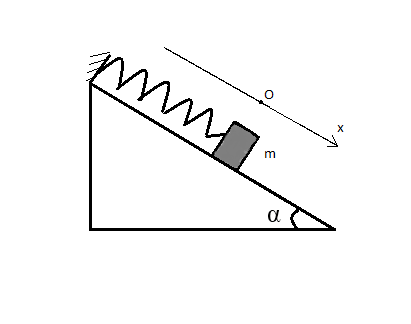
Bạn coi lại đề bài xem k=1N/m hay 100N/m.
Cho cơ hệ như hình vẽ. m 1 = 2 k g ; m 2 = 5 k g ; α = 30 ° ; β = 45 ° ; hệ số ma sát của mặt phẳng là 0,15. Lấy g = 10 m / s 2 . Gia tốc của hệ là
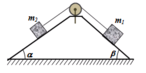
A. 1,22 m / s 2
B. 1,54 m / s 2
C. 0,32 m / s 2
D. 0,24 m / s 2
Đáp án C
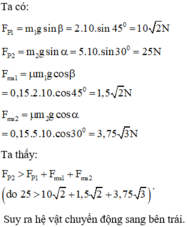
Gia tốc của hệ là
a = F P 2 − F P 1 − F m s 1 − F m s 2 m 1 + m 2 = 25 − 10 2 − 1 , 5 2 − 3 , 75 3 2 + 5 = 0 , 32 m / s 2
Tìm độ cứng của hệ hai lò xo được nối với nhau như hai hình vẽ. Hình 1, 2. Tìm độ dãn của mỗi lò xo khi treo vật m = 1kg. Biết k 1 = k 2 = 100 N m ; g = 10 m / s 2
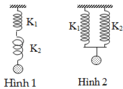 .
.
Đối với hình 1 lò xo ghép nối tiếp: Ta có F = F 1 = F 2
Mà Δ l = Δ l 1 + Δ l 2
⇒ F k = F 1 k 1 + F 2 k 2 ⇒ 1 k = 1 k 1 + 1 k 2
⇒ k = k 1 . k 2 k 1 + k 2 = 100.100 100 + 100 = 50 ( N / m )
Khi vật cân bằng P = F d h ⇒ m g = k . Δ l
⇒ 1.10 = 50. Δ l ⇒ Δ l = 0 , 2 m = 20 c m
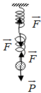
Đối với hình 1 lò xo ghép song song:
Ta có Δ l = Δ l 1 = Δ l 2
Mà F = F 1 + F 2 ⇒ k Δ l = k 1 . Δ l 1 + k 2 . Δ l 2
⇒ k = k 1 + k 2 = 100 + 100 = 200 ( N / m )
Khi vật cân bằng P = F d h ⇒ m g = k . Δ l
⇒ 1.10 = 200. Δ l ⇒ Δ l = 0 , 05 m = 5 c m
Cho cơ hệ như hình vẽ, biết hai vật m 1 = 1 k g ; m 2 = 2 k g , được nối với nhau bằng một sợi dây nhẹ không giãn, bắc qua một ròng rọc có ma sát không đáng kể. Cho g = 10 m / s 2 , Tính sức căng của sợi dây và gia tốc của cơ hệ ?
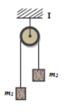
A. 10 N; 4 m / s 2
B. 15 N; 5 m / s 2
C. 13,3 N; 3,3 m / s 2
D. 12 N; 5 m / s 2
Đáp án C
Theo định luật II Niuton, ta có:
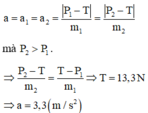
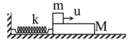
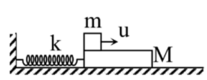
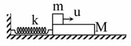
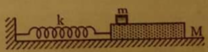
Cho cơ hệ như hình vẽ. Vật m có khối lượng 400 g được đặt trên tấm ván M dài có khối lượng 200 g. Ván nằm trên mặt phẳng nằm ngang nhẵn và được nối với giá bằng 1 lò xo có độ cứng 20 N/m. Hệ số ma sát giữa m và M là 0,4. Ban đầu hệ đang đứng yên, lò xo không biến dạng. Kéo m bằng 1 lực theo phương ngang để nó chạy đều với tốc độ u = 50 c m / s . M đi được quãng đường bao nhiêu cho đến khi nó tạm dừng lần đầu? Biết ván đủ dài. Lấy g = 10 m / s 2 .
A. 13 cm.
B. 10 cm.
C. 16 cm.
D. 8,0 cm.
Đáp án A
+ Nếu u đủ lớn, m luôn trượt trên M, M chịu tác dụng lực ma sát trượt không đổi ® M dao động điều hòa giống con lắc lò xo treo thẳng đứng có trọng lực không đổi. Vị trí cân bằng lò xo giãn:
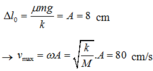
+ Khi M đuổi kịp m thì ma sát trượt chuyển thành ma sát nghỉ, M chuyển động đều với tốc độ u.
+ Khi F m s s m a x = F m s t thì m lại trượt trên M và M lại dao động điều hòa với
![]()
® Quãng đường tổng cộng đến khi dừng lại là: s = 8 + 5 = 13 c m
Cho cơ hệ như hình vẽ. Vật m có khối lượng 400 g được đặt trên tấm ván M dài có khối lượng 200 g. Ván nằm trên mặt phẳng nằm ngang nhẵn và được nối với giá bằng 1 lò xo có độ cứng 20 N/m. Hệ số ma sát giữa m và M là 0,4. Ban đầu hệ đang đứng yên, lò xo không biến dạng. Kéo m bằng 1 lực theo phương ngang để nó chạy đều với tốc độ u = 50 cm/s. M đi được quãng đường bao nhiêu cho đến khi nó tạm dừng lần đầu? Biết ván đủ dài. Lấy g = 10 m/s2.
A. 13 cm.
B. 10 cm.
C. 16 cm.
D. 8 cm.
Đán áp A
Quá trình chuyển động của vật M có thể chia thành các giai đoạn như sau:
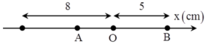
Giai đoạn thứ nhất: khi vật m trượt trên vật M, lực mà sát trượt luông không đổi, ta có thể xem chuyển động của M như dao động của vật vật chịu tác dụng của lực không đổi.
Khi đó vật M sẽ tiến về vị trí cân bằng O, với 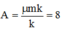 cm và tốc độ cực đại có thể đạt được khi đến O là
cm và tốc độ cực đại có thể đạt được khi đến O là ![]()
+ Giai đoạn thứ hai: trong quá trình dao động đến vị trí cân bằng O, M đi qua A, lúc này vận tốc của M tăng lên đúng bằng u = 50 cm/s, chuyển động tương đối giữa M và m là không còn, lực ma sát giữa chúng là lực ma sát nghỉ. Hai vật dính chặt vào nhau chuyển động với cùng vận tốc u = 50 cm/s.
+ Giai đoạn thứ 3: Hệ hai vật cùng chuyển động với vận tốc 50 cm/s đến O, lúc này lực đàn hồi lớn hơn lực ma sát nghỉ, vật M chậm dần và có sự chuyển động tương đối giữa M và m, bây giờ vật M được xem là dao động điều hòa dưới tác dụng của ngoại lực không đổi như giai đoạn thứ nhất. Vật M sẽ dừng lại tại biên 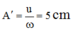
Vậy tổng quãng đường M đi được là 8 + 5 = 13 cm.
Cho cơ hệ như hình vẽ. Vật m có khối lượng 400 g được đặt trên tấm ván M dài có khối lượng 200 g. Ván nằm trên mặt phẳng nằm ngang nhẵn và được nối với giá bằng 1 lò xo có độ cứng 20 N/m. Hệ số ma sát giữa m và M là 0,4. Ban đầu hệ đang đứng yên, lò xo không biến dạng. Kéo m bằng 1 lực theo phương ngang để nó chạy đều với tốc độ u = 50 cm/s. M đi được quãng đường bao nhiêu cho đến khi nó tạm dừng lần đầu? Biết ván đủ dài. Lấy g = 10 m/ s 2 .
A. 13 cm.
B. 10 cm.
C. 16 cm.
D. 8 cm.
Đán áp A
Quá trình chuyển động của vật M có thể chia thành các giai đoạn như sau:
+ Giai đoạn thứ nhất: khi vật m trượt trên vật M, lực mà sát trượt luông không đổi, ta có thể xem chuyển động của M như dao động của vật vật chịu tác dụng của lực không đổi.
Khi đó vật M sẽ tiến về vị trí cân bằng O, với ![]() cm và tốc độ cực đại có thể đạt được khi đến O là
cm và tốc độ cực đại có thể đạt được khi đến O là ![]() cm/s
cm/s
+ Giai đoạn thứ hai: trong quá trình dao động đến vị trí cân bằng O, M đi qua A, lúc này vận tốc của M tăng lên đúng bằng u = 50 cm/s, chuyển động tương đối giữa M và m là không còn, lực ma sát giữa chúng là lực ma sát nghỉ. Hai vật dính chặt vào nhau chuyển động với cùng vận tốc u = 50 cm/s.
+ Giai đoạn thứ 3: Hệ hai vật cùng chuyển động với vận tốc 50 cm/s đến O, lúc này lực đàn hồi lớn hơn lực ma sát nghỉ, vật M chậm dần và có sự chuyển động tương đối giữa M và m, bây giờ vật M được xem là dao động điều hòa dưới tác dụng của ngoại lực không đổi như giai đoạn thứ nhất. Vật M sẽ dừng lại tại biên ![]() cm
cm
Vậy tổng quãng đường M đi được là 8 + 5 = 13 cm.
Cho hệ dao động như hình vẽ. Vật M có khối lượng 1 kg có thể chuyển động không ma sát trên mặt phẳng nằm ngang dọc theo trục của lò xo có độ cứng k = 50 N/m. Vật m có khối lương 250g đặt trên M. Hệ số ma sát nghỉ và hệ số ma sát trượt giữa vật m và M là bằng nhau và bằng μ = 0 , 3 . Cho g = 10 m / s 2 .
Vật M đủ dài để m luôn ở trên M. Ban đầu kéo hai vật đến vị trí lò xo dãn 9,5 cm rồi thả nhẹ không vận tốc đầu. Vận tốc của vật M trong quá trình chuyển động có giá trị lớn nhất là
A. 0,5930 m/s
B. 0,5060 m/s
C. 0,5657 m/s
D. 0,5692 m/s.