Học tại trường
Chưa có thông tin
Đến từ
Chưa có thông tin , Chưa có thông tin
Số lượng câu hỏi
3
Số lượng câu trả lời
2
Điểm GP
0
Điểm SP
0
Người theo dõi (1)

Đang theo dõi (1)




Chủ đề:
Bài 2. Con lắc lò xoCâu hỏi:
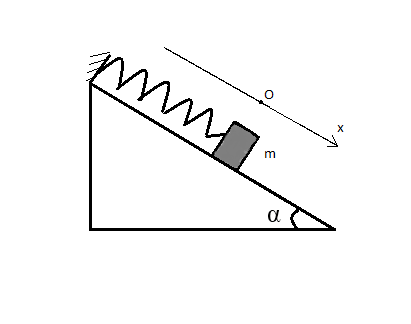
Cho con lắc lò xo như hình vẽ. Vật nhỏ khối lượng \(m=200g\), lo xo lí tưởng có độ cứng \(k=1\)N/m góc \(\alpha=30^o\). Lấy g=10m/s2
a/ Chọn trục tọa độ như hình vẽ, gốc tọa độ trùng với vị trí cân bằng. Viết phương trình dao động. Biết tại thời điểm ban đầu lò xo bị dãn 2cm và vật có vận tốc \(v_0=10\sqrt{15}\)cm/s hướng theo chiều dương.
b/ Tại thời điểm t1 lò xo không bị biến dạng, Hỏi tại \(t_2=t_1+\dfrac{\pi}{4\sqrt{5}}s\),vật có tọa độ bao nhiêu?
c/ Tính tốc độ trung bình của m trong khoảng thời gian \(\Delta t=t_2-t_1\)

Chủ đề:
Chương IV- Từ trườngCâu hỏi:
Thanh dẫn MN nằm ngang có khối lượng \(m=3g\), chiều dài \(l=20cm\), được treo bởi hai sợi dây mềm MN và QP song song như hình vẽ. Hai sợi dây cùng chiều dài,khối lượng không đáng kể, không dẫn điện. Đặt hệ thống vào trong từ trường đều có cảm ứng từ \(\overrightarrow{B}\) chiếm toàn bộ không gian chứa NP và cả vùng NP sẽ di chuyển đến. Cho dòng điện không đổi có cường độ \(I=1A\) chạy trong thanh theo chiều từ N đến P. Lấy \(g=10\)m/s2. Bỏ qua lực cản của không khí.
a) Xác định chiều va giá trị nhỏ nhất của \(\overrightarrow{B}\) để thanh NP bị đẩy lên cao theo hướng thẳng đứng
b) \(\overrightarrow{B}\) có phương thẳng đứng, chiều tư dưới lên trên, độ lớn \(B=4.10^{-2}T\). Khi NP cân bằng, mặt phẳng chứa MN và PQ lệch góc \(\alpha_0\) so với mặt phẳng thẳng đứng:
1. xác định \(\alpha_0\)
2. NP đang cân bằng, đột ngột ngắt dòng điện I. Tìm biểu thức suất điện động cảm ứng trong thanh NP khi dây treo lệch góc \(\alpha\) so với phương thẳng đứng


Chủ đề:
Chương I - Dao động cơCâu hỏi:
Một con lắc lò xo gồm lò xo nhẹ nằm ngang và mặt phẳng M. Con lắc dao động điều hòa trên trục Ox, chiều dài của lò xo thay đổi từ 20cm đến 30cm. Ở vị trí lò xo dài 30cm, độ lớn gia tốc của vật M là 8m/s2. Chọn gốc tọa độ O tại vị trí cân bằng, gốc thời gian là lúc vật M đi qua O theo chiều âm. Lấy \(\pi^2=10\)
a) Viết phương trình dao động của vật M
b) Xác định vị trí vật M khi con lắc có động năng bằng ba lần thế năng
c) Biết hiệu giữa quãng đường lớn nhất và quảng đường nhỏ nhất (vật M đi được trong cùng một khoảng thời gian \(\Delta t\)) đạt cực đại. Tính \(\Delta t\)
d) Một vật nhỏ N dao động trên trục Oy với phương trình \(y=10cos\left(4\pi t-\dfrac{\pi}{6}\right)cm\) (Ox và Oy vuông góc với nhau, O là vị trí cân bằng của cả vật N và vật M). Xác định khoảng cách giữa vật M và vật N khi vật M có li độ \(x=-2,5\sqrt{3}cm\) và đang chuyển động theo chiều âm



