Cho đường thẳng d và A là điểm nằm trên d; B là điểm nằm ngoài d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với d tại A

Những câu hỏi liên quan
Cho 3 điểm phân biệt A;B;C nằm trên đường thẳng d và điểm D không nằm trên da)Hỏi có bao nhiêu đường thẳng phân biệt đi qua ít nhất là 2 điểm trong 4 điểm A;B;C;D?Vẽ hình minh hoạ và kể tên các đường thẳng đób)Lấy thêm điểm E không nằm trên đường thẳng d và khác với điểm D.Hỏi bây giờ có bao nhiêu đường thẳng phân biệt,mỗi đường đi qua ít nhất là hai điểm trong 5 điểm A;B;C;D;E?
Đọc tiếp
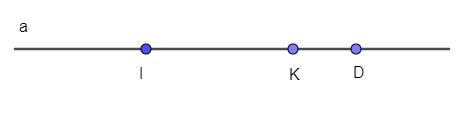
Cho 3 điểm phân biệt A;B;C nằm trên đường thẳng d và điểm D không nằm trên d
a)Hỏi có bao nhiêu đường thẳng phân biệt đi qua ít nhất là 2 điểm trong 4 điểm A;B;C;D?Vẽ hình minh hoạ và kể tên các đường thẳng đó
b)Lấy thêm điểm E không nằm trên đường thẳng d và khác với điểm D.Hỏi bây giờ có bao nhiêu đường thẳng phân biệt,mỗi đường đi qua ít nhất là hai điểm trong 5 điểm A;B;C;D;E?
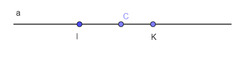
Hai điểm I, K nằm trên đường thẳng a (Hình 22).
a) Chỉ ra một điểm C trên đường thẳng a sao cho C nằm giữa I và K.
b) Chỉ ra một điểm D trên đường thẳng a sao cho K nằm giữa I và D.
Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.
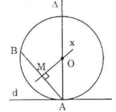
Đường tròn (O) tiếp xúc với d nên d là tiếp tuyến của (O) hay d vuông góc với bán kính của (O) tại tiếp điểm A. Suy ra tâm O của đường tròn nằm trên đường thẳng vuông góc với d tại A.
Lại có (O) qua B nên tâm O của đường tròn nằm trên đường trung trực của AB.
Vậy tâm O là giao điểm của đường vuông góc với d tại A và đường trung trực của AB.
Đúng 0
Bình luận (0)
Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.
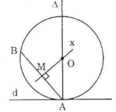
Đường tròn (O) tiếp xúc với d nên d là tiếp tuyến của (O) hay d vuông góc với bán kính của (O) tại tiếp điểm A. Suy ra tâm O của đường tròn nằm trên đường thẳng vuông góc với d tại A.
Lại có (O) qua B nên tâm O của đường tròn nằm trên đường trung trực của AB.
Vậy tâm O là giao điểm của đường vuông góc với d tại A và đường trung trực của AB.
Đúng 0
Bình luận (0)
Cho đường tròn (O; R) đường kính AB, kẻ đường thẳng d ⊥ BA tại C (C nằm giữa A và B). Lấy điểm M nằm bên ngoài đường tròn và nằm trên đường thẳng d. Gọi D là giao điểm của MA và (O); E là giao điểm của MB và (O). Tiếp tuyến của (O) tại D cắt MC tại I; H là giao điểm của AE với MC.a) Chứng minh rằng: BCHE là tứ giác nội tiếp và AH.AE AB.ACb) Chứng minh rằng: ∆DHI là tam giác cân
Đọc tiếp
Cho đường tròn (O; R) đường kính AB, kẻ đường thẳng d ⊥ BA tại C (C nằm giữa A và B). Lấy điểm M nằm bên ngoài đường tròn và nằm trên đường thẳng d. Gọi D là giao điểm của MA và (O); E là giao điểm của MB và (O). Tiếp tuyến của (O) tại D cắt MC tại I; H là giao điểm của AE với MC.
a) Chứng minh rằng: BCHE là tứ giác nội tiếp và AH.AE = AB.AC
b) Chứng minh rằng: ∆DHI là tam giác cân
a: góc HCB+góc HEB=180 độ
=>HCBE nội tiếp
Xét ΔACH vuông tại C và ΔAEB vuông tại E có
góc CAH chung
=>ΔACH đồng dạng với ΔAEB
=>AC/AE=AH/AB
=>AC*AB=AE*AH
b: góc IDH=1/2*sđ cung DB
góc IHD=90 độ-góc AMH=1/2*sđ cung DB
=>góc IDH=góc IHD
=>ΔIHD cân tại I
Đúng 0
Bình luận (0)
Vẽ hình theo diễn đạt:Vẽ đường thẳng a . Trên đường thẳng a vẽ đoạn thẳng AB 4 (cm) . Vẽ đường thẳng d đi qua điểm A và vuông góc với a . Vẽ đường thẳng d đi qua điểm B và vuông góc với .Trên đường thẳng d lấy điểm D sao cho AD AB . Trên đường thẳng d lấy điểm C sao cho hai điểm C , D nằm về cùng phía với đường thẳng a và BC AB . Vẽ các đoạn thẳng CD , AC , BD . Gọi O là giao điểm của AB và CD
Đọc tiếp
Vẽ hình theo diễn đạt:
Vẽ đường thẳng a . Trên đường thẳng a vẽ đoạn thẳng AB = 4 (cm) . Vẽ đường thẳng d đi qua điểm A và vuông góc với a . Vẽ đường thẳng d' đi qua điểm B và vuông góc với .Trên đường thẳng d lấy điểm D sao cho AD = AB . Trên đường thẳng d' lấy điểm C sao cho hai điểm C , D nằm về cùng phía với đường thẳng a và BC = AB . Vẽ các đoạn thẳng CD , AC , BD . Gọi O là giao điểm của AB và CD
Cho đường thẳng d, điểm A nằm trên đường d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A
Phân tích:
Giả sử đã dựng được đường tròn thỏa mãn đề bài.
Tâm O thỏa mãn hai điều kện:
- O nằm trên đường trung trực của AB (vì đường tròn đi qua A và B).
- O nằm trên đường thẳng vuông góc với d tại A (vì đường tròn tiếp xúc với đường thẳng d tại A).
Vậy O là giao điểm của hai đường thẳng nói trên.
Cách dựng:
- Dựng đường trung trực m của AB.
- Từ A dựng một đường thẳng vuông góc với d cắt đường thẳng m tại O.
- Dựng đường tròn (O;OA). Đó là đường tròn phải dựng.
Chứng minh:
Vì O nằm trên đường trung trực của AB nên OA=OB, do đó đường tròn (O;OA) đi qua A và B.
Đường thẳng d⊥OAd⊥OA tại A nên đường thẳng d tiếp xúc với đường tròn (O) tại A.
Biện luận: Bài toán luôn có nghiệm hình.
Đúng 0
Bình luận (0)
Cho điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Dựng đường tròn (O) đi qua A và B nhận đường thẳng d làm tiếp tuyến.
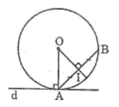
* Phân tích
- Giả sử dựng được đường tròn (O) qua A, B và tiếp xúc với d. Khi đó đường tròn (O) phải tiếp xúc với d tại A
- Đường tròn (O) đi qua A và B nên tâm O nằm trên đường trung trực của AB
- Đường tròn (O) tiếp xúc với d tại A nên điểm O nằm trên đường thẳng vuông góc với d tại điểm A
* Cách dựng
- Dựng đường thẳng trung trực của AB
- Dựng đường thẳng đi qua A và vuông góc với d. Đường thẳng này cắt đường trung trực của AB tại O
- Dựng đường tròn (O; OA) ta được đường tròn cần dựng
* Chứng minh
Vì O nằm trên đường trung trực của AB nên OA = OB. Khi đó đường tròn (O; OA) đi qua hai điểm A và B
Đúng 0
Bình luận (0)
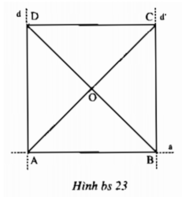
Vẽ đường thẳng a. Trên đường thẳng a vẽ đoạn thẳng AB 4 (cm). Vẽ đường thẳng d đi qua điểm A và vuông góc với a. Vẽ đường thẳng d’ đi qua điểm B và vuông góc với a. Trên đường thẳng d lấy điểm D sao cho AD AB. Trên đường thẳng d’ lấy điểm C sao cho hai điểm C, D nằm về cùng phía với đường thẳng a và BC AB. Vẽ các đoạn thẳng CD, AC, BD. Gọi O là giao điểm của AC và BD.a) Đo và cho biết số đo góc ADC.b) Đo và cho biết số đo góc BCD.C) Đo và cho biết số đo góc BOC
Đọc tiếp
Vẽ đường thẳng a. Trên đường thẳng a vẽ đoạn thẳng AB = 4 (cm). Vẽ đường thẳng d đi qua điểm A và vuông góc với a. Vẽ đường thẳng d’ đi qua điểm B và vuông góc với a. Trên đường thẳng d lấy điểm D sao cho AD = AB. Trên đường thẳng d’ lấy điểm C sao cho hai điểm C, D nằm về cùng phía với đường thẳng a và BC = AB. Vẽ các đoạn thẳng CD, AC, BD. Gọi O là giao điểm của AC và BD.
a) Đo và cho biết số đo góc ADC.
b) Đo và cho biết số đo góc BCD.
C) Đo và cho biết số đo góc BOC