Không có góc nhọn nào như vậy bởi nếu x là góc nhọn thì \(\sin x< =1;\cos x< =1\)

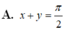
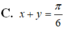
Chọn A

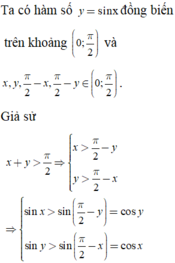
·        Bổ trợ kiến thức: Các em có thể sử dụng máy tính cầm tay VINACAL 570ES PLUS II để giải bài toán trên như sau. Giả sử cho x = 0,27 , từ phương trình đề bài:  và từ các đáp án bên dưới, ta thử từng phương án thì rõ ràng 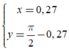 làm thỏa mãn phương trình, khi đó ta dễ dàng chọn được phương án đúng.

Các em ghi nhớ luôn nhé – để áp dụng vào các bài tập khác: “với 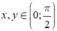thì ra luôn có ”

ĐK: \(x\ne\dfrac{\pi}{2}+k\pi\)

Ta có: 

\(\left\{{}\begin{matrix}tanx=3\\sin^2x+cos^2x=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}sinx=3cosx\\9cos^2x+cos^2x=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}sinx=3cosx\\cos^2x=\dfrac{1}{10}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}sinx=3cosx\\cosx=\pm\dfrac{1}{\sqrt{10}}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}sinx=\dfrac{3}{\sqrt{10}}\\cosx=\dfrac{1}{\sqrt{10}}\end{matrix}\right.\\\left\{{}\begin{matrix}sinx=-\dfrac{3}{\sqrt{10}}\\cosx=-\dfrac{1}{\sqrt{10}}\end{matrix}\right.\end{matrix}\right.\)

cosx = 2,3540: không có góc nhọn x vì cosx < 1

tgx = 1,6754 ⇒ x = 59 ° 10 '

Ta có: *nếu x = 45 °  thì sinx = cosx, suy ra: sinx – cosx = 0

*nếu x <  45 °  thì cosx = sin( 90 °  – x)

Vì x <  45 ° nên  90 °  – x >  45 ° , suy ra: sinx < sin( 90 °  – x)

Vậy sinx – cosx < 0

*nếu x >  45 °  thì cosx = sin( 90 °  – x)

Vì x >  45 °  nên  90 °  – x <  45 ° , suy ra: sinx > sin( 90 °  – x)

Vậy sinx – cosx > 0.