Cho tam giác nhọn ABC, hai đường cao BD và CE. Chứng minh S A D E = S A B C . cos 2 A

Những câu hỏi liên quan
Cho tam giác ABC nhọn, hai đường cao BD và CE (D=AC, E=AB). a) Chứng minh: tam giác ABD đồng dạng với tam giác ACE. b) Chứng minh: góc EDB bằng góc ECB
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc EDB=góc ECB
Đúng 0
Bình luận (0)
Cho tam giác nhọn abc(ab<ac), hai đường cao BD,CE(E thuộc AB,D thuộc AC). a)chứng minh ∆ABD~∆ACE
b)chứng minh ∆ABC~∆ADE,từ đó suy ra AD.BC=AB.DE
c)gọi giao điểm của BD và CE là H.Chứng minh BH.BD+CH.CE=BC2
a, Xét ∆ ABD và ∆ ACE có:
góc ADB = góc AEC ( = 90°)
Góc A chung
=> ∆ABD ~ ∆ ACE (g- g)
b,
Đúng 2
Bình luận (0)
Cho tam giác ABC nhọn có hai đường cao BD và CE.
1) Chứng minh bốn điểm B,C,D,E cùng thuộc một đường tròn.
2) Chứng minh OI vuông góc với DE.
1) Xét tứ giác BCDE có
\(\widehat{BEC}=\widehat{BDC}\left(=90^0\right)\)
nên BCDE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay B,C,D,E cùng thuộc 1 đường tròn(đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn, hai đường cao BD và CE của tam giác cắt nhau tại H (D thuộc AC, E thuộc AB)
a) Chứng minh rằng tam giác BHE đồng dạng với tam giác CHD
b) Chứng minh AB.AE = AC.AD
c) Chứng minh góc AED = góc ACB
a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE; AD/AB=AE/AC
c: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
=>góc AED=góc ACB
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Tia BD và tia CE cắt đường tròn (O) lần lượt tại M, N (M khác B, N khác C)a) Chứng minh bốn điểm B, C, D, E cùng nằm trên một đường tròn.b) Chứng minh DE // MNc) Đường tròn đường kính AH cắt đường tròn (O) tại điểm thứ hai là K (K khác A). Tia KH cắt đường tròn (O) tại điểm thứ hai là Q. Tứ giác BHCQ là hình gì? Tại sao?d) Gọi giao điểm của HQ và BC là I. Chứng minh OI/MN 1/4
Đọc tiếp
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Tia BD và tia CE cắt đường tròn (O) lần lượt tại M, N (M khác B, N khác C)a) Chứng minh bốn điểm B, C, D, E cùng nằm trên một đường tròn.b) Chứng minh DE // MNc) Đường tròn đường kính AH cắt đường tròn (O) tại điểm thứ hai là K (K khác A). Tia KH cắt đường tròn (O) tại điểm thứ hai là Q. Tứ giác BHCQ là hình gì? Tại sao?d) Gọi giao điểm của HQ và BC là I. Chứng minh OI/MN > 1/4
a) Gọi G là trung điểm của BC
Ta có: ΔDBC vuông tại D(BD\(\perp\)AC tại D)
mà DG là đường trung tuyến ứng với cạnh huyền BC(G là trung điểm của BC)
nên \(DG=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(1)
Ta có: ΔEBC vuông tại E(CE\(\perp\)AB)
mà EG là đường trung tuyến ứng với cạnh huyền BC(G là trung điểm của BC)
nên \(EG=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(2)
Ta có: G là trung điểm của BC(gt)
nên \(BG=CG=\dfrac{BC}{2}\)(3)
Từ (1), (2) và (3) suy ra GB=GC=GE=GD
hay B,C,D,E cùng nằm trên một đường tròn(đpcm)
Đúng 1
Bình luận (1)
Cho tam giác ABC nhọn ; có 2 đường cao BD và CE cắt nhau tại H.
a. Chứng minh rằng 4 điểm A , D , H , E thuộc 1 đường tròn.
b. Chứng minh 4 điểm B , C , E , D thuộc 1 đường tròn.
a: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=180^0\)
nên AEHD là tứ giác nội tiếp
hay A,E,H,D cùng thuộc 1 đường tròn
b: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}\)
nên BEDC là tứ giác nội tiếp
hay B,E,D,C cùng thuộc 1 đường tròn
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn và có các đường cao BD, CE. Chứng minh:
a, Các điểm B, D, C, E cùng thuộc một đường tròn
b, BC > DE
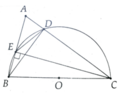
a, B,C,D,E cùng thuộc đường tròn đường kính BC
b, BC là đường kính, ED dây không qua tâm => ĐPCM
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn, hai đường cao BD và CE của tam giác cắt nhau tại H ( D thuộc AC, E thuộc AB).
a) Chứng minh 2 tam giác BHE và CHD đồng dạng
b) Chứng minh AB.AE=AC.AD
c) Chứng minh góc AED = góc ACB
cho tam giác ABC có ba góc nhọn,hai đường cao BD và CE của tam giác cắt nhau tại H (D€AC,E€AB ).Chứng minh rằng:
a) chứng minh 🔺ABC đồng dạng với tam giác AEC
b) chứng minh góc ADE= góc ABC
c) kẻ HK vuông góc BC (K€BC) .chứng minh BH.BD+CH.CE=BC mũ2
vẽ hình dùm lun nha mụi ngừi cảm ơn rất nhìu
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc BAD chung
=>ΔABD đồng dạng với ΔACE
b: ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC
Đúng 0
Bình luận (0)
cho tam giác ABC có ba góc nhọn,hai đường cao BD và CE của tam giác cắt nhau tại H (D€AC,E€AB ).Chứng minh rằng:
a) chứng minh 🔺ABC đồng dạng với tam giác AEC
b) chứng minh góc ADE= góc ABC
c) kẻ HK vuông góc BC (K€BC) .chứng minh BH.BD+CH.CE=BC mũ2
vẽ hình dùm lun nha mụi ngừi cảm ơn rất nhìu
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc ADE=góc ABC
Đúng 0
Bình luận (0)













