Cho đoạn thẳng CD
Chứng minh rằng các điểm N1, N2, N3 nằm trên đường tròn đường kính CD.
Cho đoạn thẳng CD
a) Vẽ ba điểm N 1 , N 2 , N 3 sao cho C N 1 D ^ = C N 2 D ^ = C N 3 D ^ = 90 °
b) Chứng minh rằng các điểm N 1 , N 2 , N 3 nằm trên đường tròn đường kính CD.
Vẽ Hình
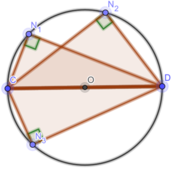
b) Vì 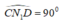 nên
nên 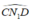 là góc nội tiếp chắn nửa đường tròn đường kính CD hay
N
1
,
nằm trên đường tròn đường kính CD
là góc nội tiếp chắn nửa đường tròn đường kính CD hay
N
1
,
nằm trên đường tròn đường kính CD
Tương tự như vậy ta chứng minh được N 2 , N 3 nằm trên đường tròn đường kính CD
Vậy N 1 , N 2 , N 3 nằm trên đường tròn đường kính CD
cho đoạn thẳng AB và điểm E nằm giữa điểm A và điểm B sao cho AE<BE.vẽ đường tròn O1 đường kính AE và đường tròn O2 đường kính BE.vẽ tiếp tuyến chung ngoài MN của hai đường tròn trên,với M là tiếp điểm thuộc (O1) và N là tiếp điểm thuộc (O2).
a )Gọi F là giao điểm của các đường thẳng AM và BN.a,chứng minh rằng đường thẳng EF vuông góc với đường thẳng AB.
b) với AB=18cm và AE=6cm,vẽ đường tròn (O) đường kính AB.đường thẳng MN cắt đường tròn (O) ở C và D,sao cho điểm C thuộc cung nhỏ AD.tính độ dài đoạn thẳng CD
làm ơn giúp mình
cho đoạn thẳng AB và điểm E nằm giữa điểm A và điểm B sao cho AE<BE.vẽ đường tròn O1 đường kính AE và đường tròn O2 đường kính BE.vẽ tiếp tuyến chung ngoài MN của hai đường tròn trên,với M là tiếp điểm thuộc (O1) và N là tiếp điểm thuộc (O2).
Gọi F là giao điểm của các đường thẳng AM và BN.a,chứng minh rằng đường thẳng EF vuông góc với đường thẳng AB.
b,với AB=18cm và AE=6cm,vẽ đường tròn (O) đường kính AB.đường thẳng MN cắt đường tròn (O) ở C và D,sao cho điểm C thuộc cung nhỏ AD.tính độ dài đoạn thẳng CD
Nhận thấy tứ giác MFNE có góc M và N vuông --> góc MFN+góc MEN= 2 vuông (*)
Lại có các tam giác AFB và MEN đồng dạng (vì có góc NME=gocFAB và góc MNE =góc FBA), suy ra góc AFB=góc MEN --> góc MFN=góc MEN (**), từ (*); (**) suy ra góc MFN=góc MEN =1 vuông
--> tứ giác MENF là hình chữ nhật, từ đó dễ dàng suy ra tiếp FE vuông góc với AB
b) Gọi I ; K lần lượt là trung điểm của O1O2 và MN. Áp dụng Talét dễ dàng tính được IK=5
--> KD^2=ID^2-IK^2 =9^2 -5^2 =56 --> CD=2.KD= 4√14
Cho nửa đường tròn tâm O đường kính AB. Điểm C nằm trên O;A. (I) tiếp xúc với nửa đường tròn (O)và tiếp xúc với các đoạn thẳng CA, CD. Gọi E là tiếp điểm của AC với (I). Chứng minh: BD=BE
Cho đoạn thẳng CD
Vẽ ba điểm N1, N2, N3 sao cho C N 1 D ^ = C N 2 D ^ = C N 3 D ^ = 90 o
Cho đoạn thẳng CD
Vẽ ba điểm N 1 , N 2 , N 3 sao cho C N 1 D ^ = C N 2 D ^ = C N 3 D ^ = 90 o
Cho đoạn thẳng CD
Vẽ ba điểm N1, N2, N3 sao cho C N 1 D ^ = C N 2 D ^ = C N 3 D ^ = 90 o
Cho đoạn thẳng CD
Vẽ ba điểm N1, N2, N3 sao cho C N 1 D ^ = C N 2 D ^ = C N 3 D ^ = 90 o
Bài : Cho đườngtròn (O), diểm A nằm bên ngoài đường tròn, kẻ các tiếp tuyến AB,AC
của đường tròn (B,C là tiếp điểm).
a) Chứng minh rằng bốn điểm O, B, A, C cùng nằm trên một đường tròn, xác định tâm của
đường tròn đó.
b) Vẽ đường kính CD, chứng minh OA // BD.
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>OBAC là tứ giác nội tiếp đường tròn đường kính OA
=>O,B,A,C cùng thuộc đường tròn đường kính OA
Tâm của đường tròn là trung điểm của OA
b: Xét (O) có
AB,AC là tiếp tuyến
DO đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
Xét (O) có
ΔBCD nội tiếp
CD là đường kính
Do đó: ΔCBD vuông tại B
=>CB\(\perp\)BD
Ta có: CB\(\perp\)BD
BC\(\perp\)OA
Do đó: OA//BD