Cho A = {x ∈ R: x + 2 ≥ 0}, B = {x ∈ R: 5 – x ≥ 0}. Khi đó A ∩ B là
A. [−2;5].
B. [−2;6].
C. [−5;2].
D. (−2;+ ∞ ).
Những câu hỏi liên quan
Cho hai tập hợp
A
{
x
∈
R
:
x
+
2
≥
0
}
,
B
{
x
∈
R
:
5
−
x
≥
0
}
Khi đó A∖B là: A. [−2; 5]. B. [−2; 6]. C. (5; +
∞
). D. (2; +
∞
)
Đọc tiếp
Cho hai tập hợp A = { x ∈ R : x + 2 ≥ 0 } , B = { x ∈ R : 5 − x ≥ 0 }
Khi đó A∖B là:
A. [−2; 5].
B. [−2; 6].
C. (5; + ∞ ).
D. (2; + ∞ )
Cho
A
x
∈
R
:
x
+
2
≥
0
,
B
x
∈
R
:
6
−
x
≥
0
.
Khi đó AB là: A. [-2;5] B. [-2;6] C....
Đọc tiếp
Cho A = x ∈ R : x + 2 ≥ 0 , B = x ∈ R : 6 − x ≥ 0 . Khi đó A\B là:
A. [-2;5]
B. [-2;6]
C. (6; + ∞ )
D. (-2; + ∞ )
A={x∈R | x-2≥0 }, B={x∈R | x-5>0}.
Tính B\A.
\(A=[2;+\infty)\) ; \(B=\left(5;+\infty\right)\)
\(\Rightarrow B\backslash A=\varnothing\)
Đúng 1
Bình luận (0)
Tìm A ∩ B, A ∪ B, A \ B, B \ A, CRA, CRB.
1. A = {x ∈ R | x ≤ 2}, B = {x ∈ R | x > 5}.
2. A = {x ∈ R | x < 0 hay x ≥ 2}, B = {x ∈ R | − 4 ≤ x < 3}.
3. A = {x ∈ R | |x − 1| < 2}, B = {x ∈ R | |x + 1| < 3}.
Bài 4. Trong các mệnh đề sau, mệnh đề nào là đúng ? Giải thích ? Phát biểu các mệnh đề đó thành lời: a) x R x2 , 0. b) x R x x2 , c) x Q 2 ,4x 1 0 . d) n N n n 2 , . e) f) x R x x2 x R x x ,5 3 1 2 , 1 0
26. Cho A = / \(x\in R\) : x +2 \(\ge\) 0 / . B= / x \(\in\) R : 5 - x \(\ge\) 0 / . Khi đó A\ B là ?
Cho A={x thuộc R | ( 2x^2-1)(x+2)(x^2-2x)(x^3+5)=0 } và B={ x thuộc Z | x^3 -4x=0} chứng minh A là tập con của B
Tồn tại các giá trị của \(a\) và \(b\) để \(\left(a-2b+1\right)x+a^2-3b+2>0\), \(\forall x\in R\), Khi đó điều kiện của tham số \(b\) là?
BPT thỏa mãn với mọi x khi và chỉ khi:
\(\left\{{}\begin{matrix}a-2b+1=0\\a^2-3b+2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2b-1\\a^2-3b+2>0\end{matrix}\right.\)
\(\Rightarrow\left(2b-1\right)^2-3b+2>0\)
\(\Leftrightarrow4b^2-7b+3>0\)
\(\Rightarrow\left[{}\begin{matrix}b>1\\b< \dfrac{3}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Cho \(A = \{ x \in \mathbb{R}|1 - 2x \le 0\} ,\)\(B = \{ x \in \mathbb{R}|x - 2 < 0\} .\)
Tìm \(A \cap B,A \cup B.\)
Tham khảo:
Ta có:
Bất phương trình \(1 - 2x \le 0\) có nghiệm là \(x \ge \frac{1}{2}\) hay \(A = [\frac{1}{2};+\infty)\)
Bất phương trình \(x - 2 < 0\) có nghiệm là \(x < 2\) hay \(B = ( - \infty ;2)\)
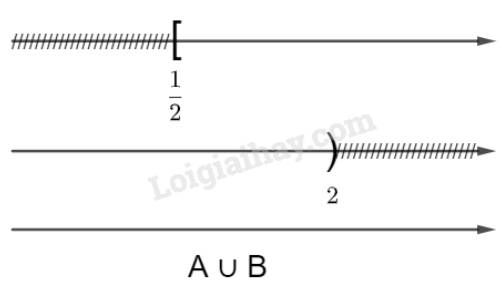
Vậy \(A \cup B = \mathbb R\)
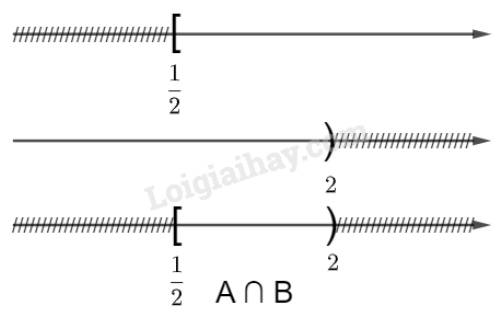
Vậy \(A \cap B = [\frac{1}{2};2)\)
Đúng 0
Bình luận (0)