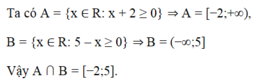Các câu hỏi tương tự
Cho hai tập hợp
A
{
x
∈
R
:
x
+
2
≥
0
}
,
B
{
x
∈
R
:
5
−
x
≥
0
}
Khi đó A∖B là: A. [−2; 5]. B. [−2; 6]. C. (5; +
∞
). D. (2; +
∞
)
Đọc tiếp
Cho hai tập hợp A = { x ∈ R : x + 2 ≥ 0 } , B = { x ∈ R : 5 − x ≥ 0 }
Khi đó A∖B là:
A. [−2; 5].
B. [−2; 6].
C. (5; + ∞ ).
D. (2; + ∞ )
Cho
A
x
∈
R
:
x
+
2
≥
0
,
B
x
∈
R
:
6
−
x
≥
0
.
Khi đó AB là: A. [-2;5] B. [-2;6] C....
Đọc tiếp
Cho A = x ∈ R : x + 2 ≥ 0 , B = x ∈ R : 6 − x ≥ 0 . Khi đó A\B là:
A. [-2;5]
B. [-2;6]
C. (6; + ∞ )
D. (-2; + ∞ )
7 tháng 10 2021 lúc 16:32
Trong các tập hợp sau, tập nào là tập con của tập nào?
a)A={1;2}, B={x∈N|x≤3},
C=[1;+∞), D={x∈R|2x2-5x+2=0}
b)A={1;3}, B={x∈Z|-1≤x≤2},
C=(0;+∞), D={x∈R|(x-1)(2-x)(x-3)=0}
7 tháng 10 2021 lúc 14:44
Bài 4.Tập hợp nào dưới đây là tập rỗng:a)A{varnothing}b)B{xinR|x2+10}c)C{xinR|x -3 và x6}Bài 5.Tìm tất cả tập con của các tập hợp sau: a)A{3;5;7}b)B{a;b;c;d}c)C{varnothing}d)D{xinR|(x-1)(x2-5x+6)0}Bài 6. Cho các tập hợp: A{a;b;c;d}, B{a;b}. Hãy tìm tất cả các tập X sao cho: BsubsetXsubsetA.
Đọc tiếp
Bài 4.Tập hợp nào dưới đây là tập rỗng:
a)A={\(\varnothing\)}
b)B={x\(\in\)R|x2+1=0}
c)C={x\(\in\)R|x< -3 và x>6}
Bài 5.Tìm tất cả tập con của các tập hợp sau:
a)A={3;5;7}
b)B={a;b;c;d}
c)C={\(\varnothing\)}
d)D={x\(\in\)R|(x-1)(x2-5x+6)=0}
Bài 6. Cho các tập hợp: A={a;b;c;d}, B={a;b}. Hãy tìm tất cả các tập X sao cho: B\(\subset\)X\(\subset\)A.
Cho các tập hợp A {x ∈ R: x2 + 4 0}; B {x ∈ R: (x2 - 4)(x2 + 1) 0}; C {-2; 2}; D {x ∈ R: |x| 2}. Khẳng định nào sau đây đúng? A. A ⊂ B. B. C ⊂ A. C. D ⊂ B. D. D ⊂ C.
Đọc tiếp
Cho các tập hợp A = {x ∈ R: x2 + 4 = 0}; B = {x ∈ R: (x2 - 4)(x2 + 1) = 0}; C = {-2; 2}; D = {x ∈ R: |x| < 2}. Khẳng định nào sau đây đúng?
A. A ⊂ B.
B. C ⊂ A.
C. D ⊂ B.
D. D ⊂ C.
Tìm A ∩ B, A ∪ B, A \ B, B \ A, CRA, CRB.
1. A = {x ∈ R | x ≤ 2}, B = {x ∈ R | x > 5}.
2. A = {x ∈ R | x < 0 hay x ≥ 2}, B = {x ∈ R | − 4 ≤ x < 3}.
3. A = {x ∈ R | |x − 1| < 2}, B = {x ∈ R | |x + 1| < 3}.
[1] Cho các tập hợp A [ -5; dfrac{1}{2} ]; B ( -3; +infty ). Khi đó tập hợp Acap B bằng:A. { x ∈ R | -3 le xledfrac{1}{2} } B. { x ∈ R | - 3 x ledfrac{1}{2} } C. { x ∈ R | -5 x ledfrac{1}{2} } D. { x ∈ R | -3 le x dfrac{1}{2}}
Đọc tiếp
[1] Cho các tập hợp A = [ -5; \(\dfrac{1}{2}\) ]; B = ( -3; \(+\infty\) ). Khi đó tập hợp \(A\cap B\) bằng:
A. { x ∈ R | -3 \(\le x\le\dfrac{1}{2}\) } B. { x ∈ R | - 3 < x \(\le\dfrac{1}{2}\) } C. { x ∈ R | -5 < x \(\le\dfrac{1}{2}\) } D. { x ∈ R | -3 \(\le x< \dfrac{1}{2}\)}
[2] Cho hai tập hợp A = { x ∈ R | 3x -1 >= 2; 3-x > 1 }; B = [ 0; 3]. Khẳng định nào sau đay là đúng?
A. \(C_BA\) = { 0; 2; 3 } B. \(C_BA\) = [ 2; 3 ] C. \(C_BA\) = [ 0; 1 ) D. \(C_BA\) = [ 0; 1 ) ∪ [ 2; 3 ]
Cho A={x thuộc R | ( 2x^2-1)(x+2)(x^2-2x)(x^3+5)=0 } và B={ x thuộc Z | x^3 -4x=0} chứng minh A là tập con của B