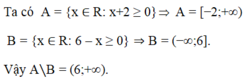Các câu hỏi tương tự
Cho A = {x ∈ R: x + 2 ≥ 0}, B = {x ∈ R: 5 – x ≥ 0}. Khi đó A ∩ B là
A. [−2;5].
B. [−2;6].
C. [−5;2].
D. (−2;+ ∞ ).
7 tháng 10 2021 lúc 14:44
Bài 4.Tập hợp nào dưới đây là tập rỗng:a)A{varnothing}b)B{xinR|x2+10}c)C{xinR|x -3 và x6}Bài 5.Tìm tất cả tập con của các tập hợp sau: a)A{3;5;7}b)B{a;b;c;d}c)C{varnothing}d)D{xinR|(x-1)(x2-5x+6)0}Bài 6. Cho các tập hợp: A{a;b;c;d}, B{a;b}. Hãy tìm tất cả các tập X sao cho: BsubsetXsubsetA.
Đọc tiếp
Bài 4.Tập hợp nào dưới đây là tập rỗng:
a)A={\(\varnothing\)}
b)B={x\(\in\)R|x2+1=0}
c)C={x\(\in\)R|x< -3 và x>6}
Bài 5.Tìm tất cả tập con của các tập hợp sau:
a)A={3;5;7}
b)B={a;b;c;d}
c)C={\(\varnothing\)}
d)D={x\(\in\)R|(x-1)(x2-5x+6)=0}
Bài 6. Cho các tập hợp: A={a;b;c;d}, B={a;b}. Hãy tìm tất cả các tập X sao cho: B\(\subset\)X\(\subset\)A.
Cho hai tập hợp
A
{
x
∈
R
:
x
+
2
≥
0
}
,
B
{
x
∈
R
:
5
−
x
≥
0
}
Khi đó A∖B là: A. [−2; 5]. B. [−2; 6]. C. (5; +
∞
). D. (2; +
∞
)
Đọc tiếp
Cho hai tập hợp A = { x ∈ R : x + 2 ≥ 0 } , B = { x ∈ R : 5 − x ≥ 0 }
Khi đó A∖B là:
A. [−2; 5].
B. [−2; 6].
C. (5; + ∞ ).
D. (2; + ∞ )
25 tháng 8 2023 lúc 10:00
cho hai tập hợp:A{xinR|x^2+x-60 hoặc 3x^2-10x+80};B{xinR|x^2-2x-20 và 2x^2-7x+60}.a) viết tập hợp A,B bằng cách liệt kê các phần tử của nó.b) tìm tất cả các tập hợp sao cho Bsubset X và Xsubset A.
Đọc tiếp
cho hai tập hợp:
A={x\(\in\)R|\(x^2\)+x-6=0 hoặc 3\(x^2\)-10x+8=0};
B={x\(\in\)R|\(x^2\)-2x-2=0 và 2\(x^2\)-7x+6=0}.
a) viết tập hợp A,B bằng cách liệt kê các phần tử của nó.
b) tìm tất cả các tập hợp sao cho \(B\subset X\) và \(X\subset A\).
Giúp với, mình cần gấp
1.Cho A= {x€ R/x ≤ -3 hoặc x>6}; B={x€ R/ x^2-25≤0}. Viết các tập hợpsau dưới dạng đoạn – khoảng- nữa khoảng
R\(A ∪ B), A ∩ B, A\B, B\A, R\(A ∩ B), R\(A\B)
7 tháng 10 2021 lúc 16:32
Trong các tập hợp sau, tập nào là tập con của tập nào?
a)A={1;2}, B={x∈N|x≤3},
C=[1;+∞), D={x∈R|2x2-5x+2=0}
b)A={1;3}, B={x∈Z|-1≤x≤2},
C=(0;+∞), D={x∈R|(x-1)(2-x)(x-3)=0}
Cho mệnh đề chứa biến P(x), với x \(\in R\). Tìm x để P(x) là mệnh đề đúng?
a) P(x): " \(x^2-5x+4=0\) "
b) P(x): " \(x^2-5x+6=0\) "
c) P(x): " \(x^2-3x>0\) "
d) P(x): "\(\sqrt{x}>x\) "
e) P(x): " 2x+ 3<7 "
f) P(x): " \(x^2+x+1>0\) "
30 tháng 9 2021 lúc 16:27
Bài 1:Cho A{xinR|x2-x-60}, B{ninN|2n-6≤0} và C{ninN||n|≤4}a)Tìm AcapB, AcapC, BcapC, AcapBcapCb)Tìm AcupB, AcupC, BcupC, AcupBcupCc)Tìm AB, AC, BCBài 2:Cho tập E{a,b,c,d}, F{b,c,e,g}, G{c,d,e,f}. CMR: Ecap(FcupG)(EcapF)cup(EcapG).
Đọc tiếp
Bài 1:Cho A={x\(\in\)R|x2-x-6=0}, B={n\(\in\)N|2n-6≤0} và C={n\(\in\)N||n|≤4}
a)Tìm A\(\cap\)B, A\(\cap\)C, B\(\cap\)C, A\(\cap\)B\(\cap\)C
b)Tìm A\(\cup\)B, A\(\cup\)C, B\(\cup\)C, A\(\cup\)B\(\cup\)C
c)Tìm A\B, A\C, B\C
Bài 2:Cho tập E={a,b,c,d}, F={b,c,e,g}, G={c,d,e,f}. CMR:
E\(\cap\)(F\(\cup\)G)=(E\(\cap\)F)\(\cup\)(E\(\cap\)G).
Bài 1. Liệt kê các phần tử của tập hợp sau:a) A {x Î N | x 6} b) B {x Î N | 1 x £ 5}c) C {x Î Z , |x| £ 3} d) D {x Î Z | x2 - 9 0}e) E {x Î R | (x - 1)(x2 + 6x + 5) 0} f) F {x Î R | x2 - x + 2 0}g) G {x Î N | (2x - 1)(x2 - 5x + 6) 0} h) H {x | x 2k với k Î Z và -3 k 13}i) I {x Î Z | x2 4 và |x| 10} j) J {x | x 3k với k Î Z và -1 k 5}k) K {x Î R | x2 - 1 0 và x2 - 4x + 3 0} l) L {x Î Q | 2x - 1 0 hay x2 - 4 0
Đọc tiếp
Bài 1. Liệt kê các phần tử của tập hợp sau:
a) A = {x Î N | x < 6} b) B = {x Î N | 1 < x £ 5}
c) C = {x Î Z , |x| £ 3} d) D = {x Î Z | x2 - 9 = 0}
e) E = {x Î R | (x - 1)(x2 + 6x + 5) = 0} f) F = {x Î R | x2 - x + 2 = 0}
g) G = {x Î N | (2x - 1)(x2 - 5x + 6) = 0} h) H = {x | x = 2k với k Î Z và -3 < k < 13}
i) I = {x Î Z | x2 > 4 và |x| < 10} j) J = {x | x = 3k với k Î Z và -1 < k < 5}
k) K = {x Î R | x2 - 1 = 0 và x2 - 4x + 3 = 0} l) L = {x Î Q | 2x - 1 = 0 hay x2 - 4 = 0