Biết hàm số y = f x = 3 x + b k h i x ≤ - 1 x + a k h i x > - 1 có giới hạn tại x= -1. Giá trị của a - b bằng
A. - 1
B. - 2
C. 2
D. 1
Những câu hỏi liên quan
Bài 1: Xét tính đơn điệu của hàm số yf(x) khi biết đạo hàm của hàm số là:a) f(x)(x+1)(1-x^2)(2x-1)^3b) f(x)(x+2)(x-3)^2(x-4)^3Bài 2: Cho hàm số yf(x) có đạo hàm f(x)x(x+1)(x-2). Xét tính biến thiên của hàm số:a) yf(2-3x)b) yf(x^2+1)c) yf(3x+1)
Đọc tiếp
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
Cho hàm số y=f(x) = 5.x Tìm x biết f(x)=0; f(x)=1; f(x)=-5; f(x)=2005
Cho hàm số y=f(x)=a.x - 3 Tìm a nếu biết f(3)=9
GIÚP MIK VS! MIK CẦN CÂU TRẢ LỜI GẤP! > . <
Cho hàm số y f(x) xác định trên
ℝ
và có đồ thị của hàm số
f
(
x
)
,
biết
f
(
3
)
+
f
(
2
)
f...
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .
Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)
Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.
Đúng 0
Bình luận (0)
1. tìm x, y biết : x/y =3/5 và 3x +y = 28
2.cho hàm số y =f(x) =ax
*khi a=2
a.vẽ đồ thị hàm số
b. tính f(-0,5);f(3/4)
*tìm hệ số a biết đò thị hàm số đi qua điểm A(-4;2)
\(1,\Rightarrow\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{3x+y}{9+5}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=6\\y=10\end{matrix}\right.\\ 2,\\ a,a=2\Rightarrow y=f\left(x\right)=2x\\ b,f\left(-0,5\right)=2\left(-0,5\right)=-1\\ f\left(\dfrac{3}{4}\right)=2\cdot\dfrac{3}{4}=\dfrac{3}{2}\\ c,\text{Thay }x=-4;y=2\Rightarrow-4a=2\Rightarrow a=-\dfrac{1}{2}\)
Đúng 3
Bình luận (0)
Ta có: x/y=3/5 ⇒ x/3=y/5
Theo tính chất của dãy tỉ số bằng nhau ta có:x/3=y/5=3x/3.3=y/5= 3x+y9/y9+5=28/14=2
Do đó:
x/3=2 ⇒x=2.3=6
y/5=2 ⇒y=2.5=10
Vậy x=6 và y=10.
Đúng 1
Bình luận (0)
Cho hàm số y f(x) xác định trên tập số thực và có đạo hàm f(x). Đồ thị hàm số y f(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) f(4). - f(3). Giá trị nhỏ nhất của hàm số y f(x) trên đoạn [0;4] là A. f(1) B. f(0) C. f(2) D. f(4)
Đọc tiếp
Cho hàm số y = f(x) xác định trên tập số thực và có đạo hàm f'(x). Đồ thị hàm số y = f'(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) = f(4). - f(3). Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0;4] là
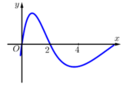
A. f(1)
B. f(0)
C. f(2)
D. f(4)
Chọn D
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
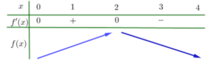
Từ bảng biến thiên, ta có nhận xét sau: 
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
Đúng 0
Bình luận (0)
20 tháng 7 2021 lúc 16:24
Bài 1 : Cho hàm số: y f(x) a.x2+b.x+c cho biết f(0)2010, f(1)2011, f(-1)2012, Tính f(-2).Bài 2 : Cho hàm số: y f(x) a.x2+b.x+c cho biết f(0)2010, f(1)2011, f(-1)2012, Tính f(-2).Bài 3 : Cho hàm số: y f(x) a.x2+b.x+c cho biết f(0)2010, f(1)2011, f(-1)2012, Tính f(-2).Bài 4 : Cho đa thức: f(x) x2-a.x-3 và g(x) (x3-x2-x-a-1)2015a, Tìm a biết -1 là 1 nghiệm của f(x)b, Với a tìm được ở câu a, Tìm nghiệm còn lại của f(x) và tính g(2).Bài 5: Cho hàm số y f(x) a.x2+b.x+c và biết f(0)2014, f(1)2015,...
Đọc tiếp
Bài 1 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 2 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 3 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 4 : Cho đa thức: f(x)= x2-a.x-3 và g(x)= (x3-x2-x-a-1)2015
a, Tìm a biết -1 là 1 nghiệm của f(x)
b, Với a tìm được ở câu a, Tìm nghiệm còn lại của f(x) và tính g(2).
Bài 5: Cho hàm số y= f(x)= a.x2+b.x+c và biết f(0)=2014, f(1)=2015, f(-1)=2017 ,
Tính f(-2).
Mọi người giúp mình với ạ mình đang cần gấp. Mình cảm ơn mọi người nhiều.
Bài 1 : làm tương tự với bài 2;3 nhé
Ta có : \(f\left(0\right)=c=2010;f\left(1\right)=a+b+c=2011\)
\(\Rightarrow f\left(1\right)=a+b=1\)
\(f\left(-1\right)=a-b+c=2012\Rightarrow f\left(-1\right)=a-b=2\)
\(\Rightarrow a+b=1;a-b=2\Rightarrow2a=3\Leftrightarrow a=\dfrac{3}{2};b=\dfrac{3}{2}-2=-\dfrac{1}{2}\)
Vậy \(f\left(-2\right)=4a-2b+c=\dfrac{4.3}{2}-2\left(-\dfrac{1}{2}\right)+2010=6+1+2010=2017\)
Đúng 4
Bình luận (0)
Cho hàm số y f(x). Biết hàm số y f(x) có đồ thị như hình vẽ bên dưới. Hàm số
y
3
-
x
2
đồng biến trên khoảng A. (0;1) B. (-1;0) C. (2;3) D. (-2;-1)
Đọc tiếp
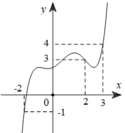
Cho hàm số y = f(x). Biết hàm số y = f(x) có đồ thị như hình vẽ bên dưới. Hàm số y = 3 - x 2 đồng biến trên khoảng
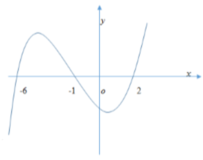
A. (0;1)
B. (-1;0)
C. (2;3)
D. (-2;-1)
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f(x), biết f(3)+f(20f(0)+f(1) và các khẳng định sau:1) Hàm số yf(x) có 2 điểm cực trị2) Hàm số yf(x) đồng biến trên khoảng
-
∞
;
0
3)
M
a
x
0
;
3
f...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là
A. 2
B. 3
C. 4
D. 5
Cho hàm số yf(x). Hàm số y f’(x) có đồ thị như hình vẽ dưới đây. Đặt
g
(
x
)
2
f
(
x
)
-
x
+
1
2
.Biết f(-2)f(3). Mệnh đề nào đúng? A. B C. D.
Đọc tiếp
Cho hàm số y=f(x). Hàm số y= f’(x) có đồ thị như hình vẽ dưới đây.
Đặt g ( x ) = 2 f ( x ) - x + 1 2 .Biết f(-2)=f(3). Mệnh đề nào đúng?
A. 
B
C. 
D. 
Câu 1: Cho hàm số y = 2x\(^2\)
a) Hãy lập bảng tính các giá trị f(-5), f(-3), f(0), f(3), f(5)
b) Tìm x biết f(x) = 8, f(x) = 6 - 4\(\sqrt{2}\)
Câu 2: Cho hàm số y = f(x) = \(\dfrac{1}{3}x^2\)
Tìm các giá trị của x, biết rằng \(y=\dfrac{1}{27}\). Cũng câu hỏi tương tự với y = 5
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
Đúng 2
Bình luận (0)