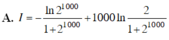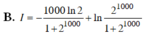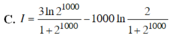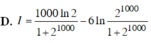Tính tích phân I = ∫ - 1 1 x 3 + x 2 - x - 1 d x ta được kết quả I = a b , khi đó tổng a + b là:
A. 7.
B. 3.
C. 5.
D. 9.
Cho ∫ - 1 / 2 1 f ( x ) dx = 3 . Tính tích phân I = ∫ 0 π 3 f ( cos 2 x ) sin 2 xdx
A. 3
B. 2 3
C. -3
D. 3 2
Tính tích phân I = ∫ 0 1 ( x - 3 ) 8 ( 2 x + 1 ) 10 d x ta được
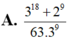
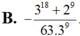
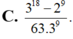
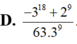
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Tính tích phân : \(I=\int\limits^2_0\frac{x^5}{\sqrt{x^3+1}}dx\)
Ta có :\(I=\int\limits^2_0\frac{x^2x^3}{\sqrt{x^3+1}}dx\)
Đặt \(t=\sqrt{x^3+1}\) khi đó với x=0 thì t=1,x=2 thì t=3
và \(dt=\frac{3x^2}{2\sqrt{x^3+1}}dx\Rightarrow\frac{x^2}{\sqrt{x^3+1}}dx=\frac{2}{3}dt,x^3=t^2-1\)
Suy ra \(I=\frac{2}{3}\int\limits^3_1\left(t^2-1\right)dt=\frac{2}{3}\left(\frac{1}{3}t^2-t\right)|^3_1=\frac{2}{3}\left(\frac{26}{3}-2\right)=\frac{40}{9}\)
Vậy \(I=\int\limits^2_0\frac{x^5}{\sqrt{x^3+1}}dx=\frac{40}{9}\)
Tính tích phân : \(I=\int\limits_{\frac{-1}{2}}^0\frac{dx}{\left(x+1\right)\sqrt{3+2x-x^2}}\)
\(I=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)\sqrt{3+2x-x^2}}=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)\left(\sqrt{\left(x+1\right)\left(3-x\right)}\right)}\)
\(=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)^2\sqrt{\frac{3-x}{x+1}}}\)
Đặt \(t=\sqrt{\frac{3-x}{x+1}}\Rightarrow\frac{dx}{\left(x+1\right)^2}=-\frac{1}{2}\)
Đổi cận : \(x=-\frac{1}{2}\Rightarrow t=\sqrt{7};x=0\Rightarrow t=\sqrt{3}\)
\(I=-\frac{1}{2}\int\limits^{\sqrt{3}}_{\sqrt{7}}dt=\frac{1}{2}\left(\sqrt{7}-\sqrt{3}\right)\)
Tính tích phân :
\(I=\int\limits^1_0\frac{dx}{\left(x+1\right)^3}\)
\(I=\int\limits^1_0\frac{x+1-1dx}{\left(x+1\right)^3}=\int\limits^1_0\frac{dx}{\left(x+1\right)^2}-\int\limits^1_0\frac{dx}{\left(x+1\right)^3}=x+1|^1_0+\frac{1}{2\left(x+1\right)^2}|^1_0=\frac{1}{8}\)
Cho f(x) xác định và liên tục trên ℝ , biết f(1)=2, f(3)=4. Tính tích phân I = ∫ 1 2 2 f ' x − x d x .
A. I = 0.
B. I = 1.
C. I = -2.
D I = 2.
Tính tích phân bất định :
\(I=\int\frac{dx}{\sqrt{\left(1+x^2\right)^3}}\)
Tính tích phân I= ∫ 1 2 100 ln x ( x + 1 ) 2 d x , ta được kết quả
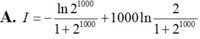
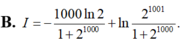
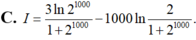
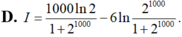
Tính tích phân I = ∫ 1 2 1000 ln x ( x + 1 ) 2 d x , ta được kết quả