+ Vì 11 ≠ 0 (luôn đúng) nên phân thức x 2 − 9 11  luôn có nghĩa.

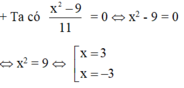
Vậy có hai giá trị của x thỏa mãn yêu cầu đề bài: x = 3; x = -3.

Đáp án cần chọn là: B

Xét biểu thức

A = ( x + 1 ) x 2 + 2 = 0 ⇔ x + 1 = 0 x 2 + 2 = 0 ⇒ x + 1 = 0  do  x 2 + 2 ≥ 2 > 0 ⇒ x = − 1

Vậy có 1 giá trị của x thỏa mãn

Chọn đáp án B

a: Khi x=-1 thì \(y=2^{-1}=\dfrac{1}{2}\)

Khi x=0 thì \(y=2^0=1\)

Khi x=1 thì \(y=2^1=2\)

Với mỗi giá trị của x thì chỉ có 1 giá trị 2^x tương ứng

b: Biểu thức y=2^x có nghĩa với mọi x

Đáp án C

Đặt t = log 2 x  với x ∈ 0 ; + ∞  thì t ∈ ℝ , khi đó bất phương trình trở thành  t 2 + m t - m > 0 *

Để (*) nghiệm đúng với mọi t ∈ ℝ ⇔ ∆ * ≤ 0 ⇔ m 2 + 4 m ≤ 0 ⇔ m ∈ - 4 ; 0  

Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện

Đáp án cần chọn là: B

Đáp án cần chọn là: D