Cho tích phân I = ∫ 0 1 3 x + 3 ln 3 x + 1 x + 1 2 d x = = ∫ 0 1 a 3 x + ! - b x + 1 d x .Tính
A = a 2 - b 2 . Chọn đáp án đúng:
A. 0
B. 2
C. 3
D. 4
Tính các tích phân sau: 1) 2 ln e e x dx ; 2) 1 3 2 0 4 x dx x ; 3) /2 /4 1 tan dx x ; 4) 1 0 x e dx ; 5) 2 1 x xe dx ; 6) 0 1 3 4 dx x ; 7) 2 1 4 4 5 dx x x ; 8) 2 0 ln 1 x dx x (HD: 1 u x ) ĐS: 1) 2 e ; 2) 16 7 5 3 ; 3) ln 2 ; 4) 2
Tính tích phân :
\(I=\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{3}}\frac{\ln\left(4\tan x\right)}{\sin2x.\ln\left(2\tan x\right)}dx\)
Ta có \(I=\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{4}}\frac{\ln2.\ln\left(2\tan x\right)}{\sin2x.\ln\left(2\tan x\right)}dx=\ln2\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{4}}\frac{dx}{\sin2x.\ln\left(2\tan x\right)}+\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{4}}\frac{dx}{\sin2x}\)
Tính \(\ln2\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{4}}\frac{dx}{\sin2x.\ln\left(2\tan x\right)}=\frac{\ln2}{2}\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{4}}\frac{d\left[\ln\left(2\tan x\right)\right]}{\ln2\left(2\tan x\right)}=\frac{\ln2}{2}\left[\ln\left(\ln\left(2\tan x\right)\right)\right]|^{\frac{\pi}{3}}_{\frac{\pi}{4}}=\frac{\ln2}{2}.\ln\left(\frac{\ln2\sqrt{3}}{\ln2}\right)\)
Tính \(\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{4}}\frac{dx}{\sin2x}=\frac{1}{2}\ln\left(\tan x\right)|^{\frac{\pi}{3}}_{\frac{\pi}{4}}=\frac{1}{2}\ln\sqrt{3}\)
Vậy \(I=\frac{\ln2}{2}\ln\left(\frac{\ln2\sqrt{3}}{\ln2}\right)+\frac{1}{2}\ln\sqrt{3}\)
Hỏi phương trình 3x2- 6x+ ln( x+1) 3+1=0 có bao nhiêu nghiệm phân biệt?
A. 2.
B. 1.
C. 3.
D. 4.
Điều kiện: x> -1
Ta có: 3x2- 6x+ ln( x+1) 3+1=0 hay 3x2- 6x+ 3ln( x+1)+1=0
f(x)=3x2- 6x+ 3ln( x+1) +1=0 ⇒ f ' ( x ) = 6 x - 6 + 3 x + 1
Đạo hàm f’ (x) = 0 khi và chỉ khi (2x- 2) (x+ 1) +1=0
⇔ x = ± 1 2
Từ đây, ta có bảng biến thiên của f(x):
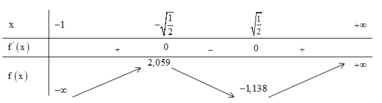
Nhìn vào bảng biến thiên ta sẽ có phương trình đã cho có 3 nghiệm phân biệt.
Chọn C.
Khảo sát sự hội tụ phân kỳ của tích phân suy rộng
\(\int\limits^{\infty}_0\dfrac{\ln\left(\sqrt[3]{1+\dfrac{3}{4}x^{200}}\right)}{x^2}dx\)
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Tính tích phân I = ∫ 1 2 4 x + 3 . ln x d x = 7 ln a + b . Tính sin a + b π 4
A. 1
B. - 1
C. 0
D. 1 2
Tính tích phân :
\(\int\limits^3_1\frac{3+\ln x}{\left(x+1\right)^2}dx\)
Tính tích phân của hàm số chứa Ln:
\(I=\int_{\varepsilon}^{\varepsilon^2}\left(\frac{1}{\ln^2x}-\frac{1}{\ln x}\right)dx\)
MỌI NGƯỜI GIÚP MÌNH CÂU TÍCH PHÂN NÀY VỚI!!!!!!!!
đặt t = lnx
tôi ko biết \(\varepsilon\) trong bài là gì, tuy nhiên nếu nó là số bất kì thì xét 2 TH sau để biết đk t
TH1: \(\varepsilon\in\left(0;1\right)\)
TH2: \(\varepsilon>1\)
Đề bài
Giải mỗi bất phương trình sau:
a) \({5^x} < 0,125\)
b) \({\left( {\frac{1}{3}} \right)^{2x + 1}} \ge 3\)
c) \({\log _{0,3}}x > 0\)
d) \(\ln (x + 4) > \ln (2x - 3)\)
\(a,5^x< 0,125\\ \Leftrightarrow x< -1,292\\ b,\left(\dfrac{1}{3}\right)^{2x+1}\ge3\\ \Leftrightarrow2x+1\le-1\\ \Leftrightarrow2x\le-2\\ \Leftrightarrow x\le-1\)
c, Điều kiện: x > 0
\(log_{0,3}x>0\\ \Leftrightarrow x>1\)
d, Điều kiện: \(x>\dfrac{3}{2}\)
\(ln\left(x+4\right)>ln\left(2x-3\right)\\ \Rightarrow x+4>2x-3\\ \Leftrightarrow x< 7\)
Vậy \(\dfrac{3}{2}< x< 7\)
Tính tích phân :
\(I=\int\limits^4_1\frac{x^3+\ln\left(5-x\right)}{x^2}dx\)
\(I=\int_1^4\frac{\ln\left(5-x\right)+x^3}{x^2}dx=\int\limits_1^4\frac{\ln\left(5-x\right)}{x^2}dx+\int\limits^4_1xdx=I_1+I_2\)
\(I_1=\int_1^4\frac{\ln\left(5-x\right)}{x^2}dx:\)\(\begin{cases}u=\ln\left(5-x\right)\\v'=\frac{1}{x^2}\end{cases}\)\(\Rightarrow\begin{cases}u'=-\frac{1}{5-x}\\v=-\frac{1}{x}\end{cases}\)
\(I_1=-\frac{1}{x}\ln\left(5-x\right)|^4_1-\int\limits^4_1\frac{1}{x\left(5-x\right)}dx\)\(=2\ln2+\frac{1}{5}\int\limits^4_1\left(\frac{1}{x-5}-\frac{1}{x}\right)dx\)
\(=2\ln2-\frac{4}{5}\ln2=\frac{6}{5}\ln2\)
\(I_2=\int\limits^4_1xdx=\frac{x^2}{2}|^4_1=\frac{15}{2}\)
\(I=\frac{15}{2}+\frac{6}{5}\ln2\)