Biết M 0 ; 2 , N 2 ; − 2 là các điểm cực trị của đồ thị hàm số y = a x 3 + b x 2 + c x + d . Tính giá trị của hàm số tại x = − 1.
A. y − 1 = 3 .
B. y − 1 = − 3 .
C. y − 1 = − 2 .
D. y − 1 = 2 .
tìm m>0 va n>0 biết : m/n =1.357 và m^2 - n^2 = 2,468
Tìm x biết :
a, ( x + 5 ) . ( x - 4 ) = 0
b, x . ( x + 1 ) = 0
Tìm số nguyên x biết :
( x + 2 ) . ( x + 5 ) > 0
a/ \(\left(x+5\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\x-4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=4\end{matrix}\right.\)
Vậy ........
b/ \(x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
c/ \(\left(x+2\right)\left(x+5\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+2< 0\\x+5< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x+5>0\\x+2>0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< -2\\x< -5\end{matrix}\right.\\\left\{{}\begin{matrix}x>-5\\x>-2\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x< -5\\x>-2\end{matrix}\right.\)
Vậy ..
Tìm tất cả các giá trị thực của tham số m để phương trình \(x^3-3x+2-2m=0\) có ba nghiệm thực phân biệt.
A.0<m<4
B.0<m<2
C.0≤m≤4
D.0≤m≤2
Có bạn hay thầy cô nào biết giải thì giải dùm mình luôn ạ.
\(x^3-3x+2-2m=0\)
=>\(2m=x^3-3x+2\)
Chúng ta sẽ vẽ đồ thị \(y=x^3-3x+2\)
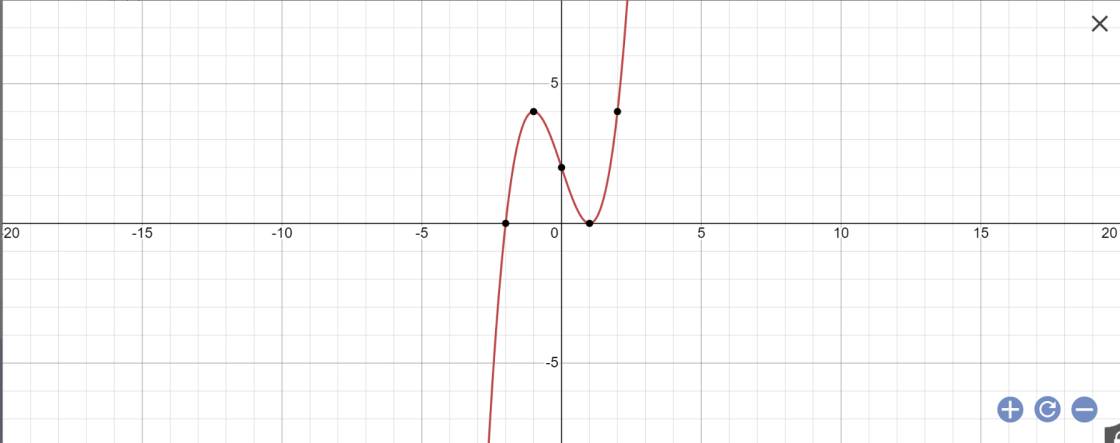
Trên đồ thị, chúng ta sẽ thấy khi \(y\in\left(0;4\right)\) thì \(y=x^3-3x+2\) sẽ cho 3 nghiệm phân biệt
=>\(2m\in\left(0;4\right)\)
=>\(m\in\left(0;2\right)\)
=>Chọn B
Biết rằng phương trình m x 2 + (3m − 1)x + 2m − 1 = 0 (m ≠ 0) luôn có nghiệm x 1 ; x 2 với mọi m. Tìm x 1 ; x 2 theo m
A. x 1 = − 1 ; x 2 = 1 − 2 m m
B. x 1 = 1 ; x 2 = 2 m − 1 m
C. x 1 = 1 ; x 2 = 1 − 2 m m
D. x 1 = − 1 ; x 2 = 2 m − 1 m
Phương trình m x 2 + (3m − 1)x + 2m − 1 = 0 (m 0) có
a = m; b = 3m – 1; c = 2m – 1
Vì a – b + c = m – 3m + 1 + 2m – 1 = 0 nên phương trình có hai nghiệm
x 1 = − 1 ; x 2 = 1 − 2 m m
Đáp án: A
tìm m biết, m - 5/ m+3 > 0
\(\frac{m-5}{m+3}>0\)
\(\Rightarrow\hept{\begin{cases}m-5>0\\m+3>0\end{cases}}\) hoặc \(\hept{\begin{cases}m-5< 0\\m+3< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m>5\\m>-3\end{cases}}\) hoặc \(\hept{\begin{cases}m< 5\\m< -3\end{cases}}\)
=> -3 > m > 5
=.= hk tốt!!
\(\frac{m-5}{m+3}>0\)
th1 :
\(\hept{\begin{cases}m-5>0\\m+3>0\end{cases}\Rightarrow\hept{\begin{cases}m>5\\m>-3\end{cases}\Rightarrow}m>5}\)
th2 :
\(\hept{\begin{cases}m-5< 0\\m+3< 0\end{cases}\Rightarrow\hept{\begin{cases}m< 5\\m< -3\end{cases}\Rightarrow}m< 5\left(m\ne-3\right)}\)
1. Tìm giá trị lớn nhất của biểu thức T, biết T = (x-13)2 - 26
2. Tìm giá trị lớn nhất của biểu thức M, biết M = 20 - (x-14)2
3. Tìm m và n biết (20 - m - n)2 + (m - 13)2 <= 0
4. Tìm y biết: (20 + y)2 -144 = 0
5. Tìm Z biết: (Z - 15)2 + 37 = 0
1.
Ta thấy $(x-13)^2\geq 0$ với mọi $x$
$\Rightarrow T=(x-13)^2-26\geq 0-26=-26$
Vậy GTNN của $T$ là $-26$.
Giá trị này đạt tại $x-13=0\Leftrightarrow x=13$
2.
Ta thấy: $(x-14)^2\geq 0$ với mọi $x$
$\Rightarrow M=20-(x-14)^2\leq 20-0=20$
Vậy $M_{\max}=20$. Giá trị này đạt tại $x-14=0$
Hay $x=14$.
3.
Ta thấy: $(20-m-n)^2\geq 0$ với mọi $m,n$
$(m-13)^2\geq 0$ với mọi $m$
$\Rightarrow (20-m-n)^2+(m-13)^2\geq 0$ với mọi $m,n$
Do đó để $(20-m-n)^2+(m-13)^2\leq 0$ thì:
$(20-m-n)^2+(m-13)^2=0$
Điều này xảy ra khi $(20-m-n)^2=(m-13)^2=0$
$\Leftrightarrow m=13; m+n=20\Leftrightarrow m=13; n=7$
1. Tìm \(m\in\left[-10;10\right]\) để pt \(\left(x^2-2x+m\right)^2-2x^2+3x-m=0\) có 4 ng pb
2. Cho biết x1,x2 là nghiệm của pt \(x^2-x+a=0\) và x3,x4 là nghiệm của pt \(x^2-4x+b=0\) . Biết rằng \(\dfrac{x2}{x1}=\dfrac{x3}{x2}=\dfrac{x4}{x3}\), b >0 . Tìm a
1.
Đặt \(x^2-2x+m=t\), phương trình trở thành \(t^2-2t+m=x\)
Ta có hệ \(\left\{{}\begin{matrix}x^2-2x+m=t\\t^2-2t+m=x\end{matrix}\right.\)
\(\Rightarrow\left(x-t\right)\left(x+t-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=t\\x=1-t\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=x^2-2x+m\\x=1-x^2+2x-m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-x^2+3x\\m=-x^2+x+1\end{matrix}\right.\)
Phương trình hoành độ giao điểm của \(y=-x^2+x+1\) và \(y=-x^2+3x\):
\(-x^2+x+1=-x^2+3x\)
\(\Leftrightarrow x=\dfrac{1}{2}\Rightarrow y=\dfrac{5}{4}\)
Đồ thị hàm số \(y=-x^2+3x\) và \(y=-x^2+x+1\):
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi \(m< \dfrac{5}{4}\)
Mà \(m\in\left[-10;10\right]\Rightarrow m\in[-10;\dfrac{5}{4})\)
tìm số nguyên m biết m-[5-m]+9=0
Cho hàm số y=f(x)=ax2+bx+c
a, Xác định a,b,c biết f(0)=5;f(1)=0;f(5)=0
b, Tìm x biết y=-3
a) Ta có: \(f\left(0\right)=5\Rightarrow a.0^2+b.0+c=5\)
\(\Rightarrow c=5\)
\(f\left(1\right)=0\Rightarrow a.1^2+b.1+c=0\)
\(\Rightarrow a+b+c=0\left(1\right)\)
Thay \(c=5\) vào (1) được:
\(a+b+5=0\Rightarrow a+b=-5\left(2\right)\)
\(f\left(5\right)=0\Rightarrow a.5^2+5b+c=0\)
\(\Rightarrow25a+5b+c=0\)
\(\Rightarrow5\left(5a+b+1\right)=0\)
\(\Rightarrow5a+b+1=0\)
\(\Rightarrow5a+b=-1\)
\(\Rightarrow b=-1-5a\left(3\right)\)
Thay \(\left(3\right)\rightarrow\left(2\right):a+\left(-1-5a\right)=-5\)
\(\Rightarrow a-1-5a=-5\)
\(\Rightarrow-1-4a=-5\)
\(\Rightarrow4a=4\)
\(\Rightarrow a=1\)
Khi đó: \(1+b=-5\Rightarrow b=-6\)
Vậy \(\left\{{}\begin{matrix}a=1\\b=-6\\c=5\end{matrix}\right.\).
b) Kết hợp \(y=-3\) với câu a) ta có:
\(x^2-6x+5=-3\)
\(\Rightarrow x^2-3x-3x+5=-3\)
\(\Rightarrow x^2-3x-3x+ 9-4=-3\)
\(\Rightarrow x\left(x-3\right)-3\left(x-3\right)-4=-3\)
\(\Rightarrow\left(x-3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x-3=1\\x-3=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\).
a) thay f(0) = 5 vào hàm số ta có : \(5=a0^2+b0+c\) \(\Leftrightarrow\) \(c=5\)
thay f(1) = 0 và f(5) = 0 vào hàm số ta có hệ phương trình
\(\left\{{}\begin{matrix}a+b+5=0\\25a+5b+5=0\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}a+b=-5\\25a+5b=-5\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}5a+5b=-25\\25a+5b=-5\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}20a=20\\a+b=-5\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=1\\1+b=-5\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=1\\b=-6\end{matrix}\right.\)
vậy \(a=1;b=-6;c=5\)
Cho m = a.b.c^2 với a,b,a,b,c € z .biết m<0 ,a>0 ,c<0 . hãy so sánh b với số 0